
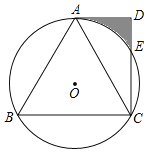
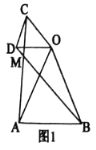
【题目】如图,⊙O为等边△ABC的外接圆,AD∥BC,∠ADC=90°,CD交⊙O于点E.
(1)求证:AD是⊙O的切线;
(2)若DE=2,求阴影部分的面积.
【答案】(1)见解析;(2)6![]() ﹣
﹣![]()
【解析】
(1)连接AO并延长交BC于F,易知AF⊥BC,根据AD∥BC可得AD⊥OA, 进而可得结论;
(2)连接AE、OE,易证AF∥CD,则∠ACD=∠CAF=![]() ∠BAC=30°,从而∠AOE=60°,进而可证明△AOE是等边三角形,于是OA=AE,∠OAE=60°,可得∠DAE=30°,然后由30°角的直角三角形的性质可得AE与AD的长,再根据阴影部分的面积=梯形OADE的面积﹣扇形AOE的面积,代入相关数据计算即得答案.
∠BAC=30°,从而∠AOE=60°,进而可证明△AOE是等边三角形,于是OA=AE,∠OAE=60°,可得∠DAE=30°,然后由30°角的直角三角形的性质可得AE与AD的长,再根据阴影部分的面积=梯形OADE的面积﹣扇形AOE的面积,代入相关数据计算即得答案.
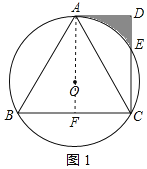
(1)证明:连接AO并延长交BC于点F,如图1所示,
∵△ABC是等边三角形,
∴AF⊥BC,
∵AD∥BC,
∴AD⊥OA,
∴AD是⊙O的切线;
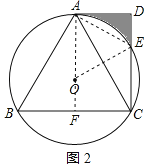
(2)解:连接AE、OE,如图2所示,
∵△ABC是等边三角形,
∴∠BAC=60°,
∵∠ADC=90°,
∴CD⊥AD,
∴AF∥CD,
∴∠ACD=∠CAF=![]() ∠BAC=30°,
∠BAC=30°,
∴∠AOE=2∠ACD=60°,
∵OA=OE,
∴△AOE是等边三角形,
∴OA=AE,∠OAE=60°,
∴∠DAE=30°,
∵∠ADC=90°,
∴OA=AE=2DE=4,AD=![]() DE=2
DE=2![]() ,
,
∴阴影部分的面积=梯形OADE的面积﹣扇形AOE的面积=![]() (2+4)×2
(2+4)×2![]() ﹣
﹣![]() =6
=6![]() ﹣
﹣![]() .
.


科目:初中数学 来源: 题型:
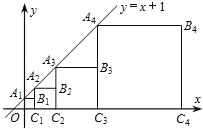
【题目】如图,直线 y=x+1 与 y 轴交于点 A1,以 OA1为边,在 y 轴右侧作正方形 OA1B1C1,延长 C1B1交直线 y=x+1 于点 A2,再以 C1A2为边作正方形,…,这些正方形与直线 y=x+1 的交点分别为 A1,A2,A3,…,An,则点 Bn 的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李叔叔和张阿姨栽树.李叔叔栽6棵树所用的时间与张阿姨栽5棵树所用的时间相同,已知李叔叔比张阿姨平均每天多栽20棵树.
(1)求李叔叔平均每天栽树的棵数;
(2)由李叔叔和张阿姨同时栽树1540棵,要几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
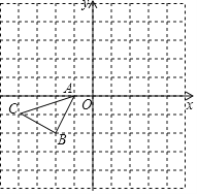
【题目】如图,方格纸中的每个小正方形的边长都为1,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)以点A为旋转中心,将△ABC绕点A顺时针旋转90°得到△AB1C1,画出△AB1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2,若点B的坐标为(-2,-2),则点B2的坐标为_________.
(3)若△A2B2C2可看作是由△AB1C1绕点P顺时针旋转90°得到的,则点P的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的![]() ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
A.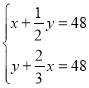 B.
B.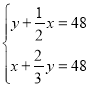 C.
C.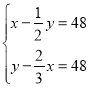 D.
D.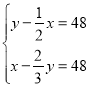
查看答案和解析>>
科目:初中数学 来源: 题型:
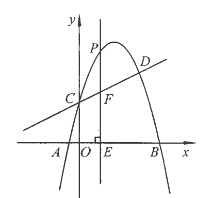
【题目】如图,抛物线![]() 与直线
与直线![]() 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为![]() 。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由;
(3)若存在点P,使∠PCF=450,请直接写出相应的点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,矩形ABCD的顶点A、D在圆上, B、C两点在圆内,已知圆心O,请仅用无刻度的直尺作图,请作出直线l⊥AD;
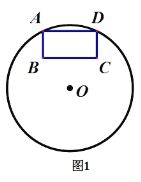
(2)请仅用无刻度的直尺在下列图2和图3中按要求作图.(补上所作图形顶点字母)
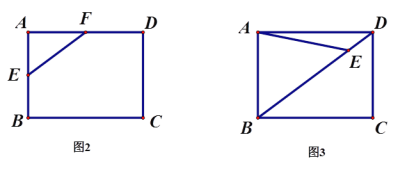
①图2是矩形ABCD,E,F分别是AB和AD的中点,以EF为边作一个菱形;
②图3是矩形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边作一个平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:
如图1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .
.
填空:①![]() 的值为 ;②
的值为 ;②![]() 的度数为 .
的度数为 .
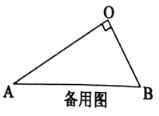
(2)类比探究:如图2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请求出
.请求出![]() 的值及
的值及![]() 的度数,并说明理由;
的度数,并说明理由;
(3)拓展延伸:在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 、
、![]() 所在直线交于点
所在直线交于点![]() ,若
,若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
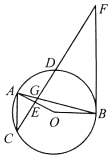
【题目】如图,点A,B,C三点均在⊙O上,⊙O外一点F,有OA⊥CF于点E,AB与CF相交于点G,有FG=FB,AC∥BF.
(1)求证:FB是⊙O的切线.
(2)若tan∠F=![]() ,⊙O的半径为
,⊙O的半径为![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com