
【题目】为了了解某校初三学生每周平均阅读时间的情况,随机抽查了该校初三m名学生,对其每周平均课外阅读时间进行统计,绘制了条形统计图和扇形统计图.
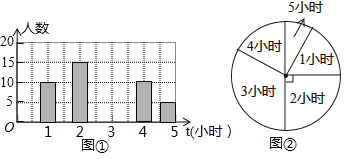
根据以上信息回答下列问题:
(1)求m的值;
(2)求扇形统计图中阅读时间为3小时的扇形圆心角的度数;
(3)求出这组数据的平均数.(精确到0.1)
【答案】(1)m=60;(2)120°;(3)2.8小时.
【解析】
(1)根据2小时所占扇形的圆心角的度数确定其所占的百分比,然后根据条形统计图中2小时的人数求得m的值;
(2)先求出课外阅读3小时的人数,再用360°乘以阅读时间为3小时的人数所占的百分比即可;
(3)利用平均数的计算公式进行计算即可.
(1)∵课外阅读时间为2小时的所在扇形的圆心角的度数为90°,
∴其所占的百分比为![]() ,
,
∵课外阅读时间为2小时的有15人,
∴m=15÷![]() =60;
=60;
(2)课外阅读3小时的人数有:60﹣10﹣15﹣10﹣5=20(人),
所以阅读时间为3小时的扇形圆心角的度数是![]() ×360°=120°;
×360°=120°;
(3)这组数据的平均数为:![]() ≈2.8小时.
≈2.8小时.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=x+1与抛物线![]() 相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.
相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.
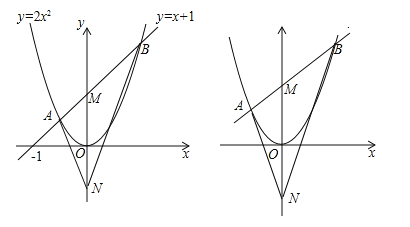
(1)①求A、B的坐标;②求证:∠ANM=∠BNM;
(2)如图2,将题中直线y=x+1变为y=kx+b(b>0),抛物线![]() 变为
变为![]() (a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
(a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E对角线AC上一点,连接DE.
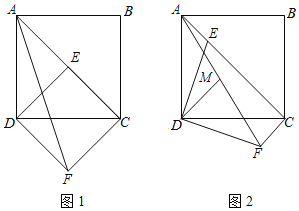
(1)如图1,若E为对角线AC中点,过点C、D分别作AC、DE的垂线相交于点F,连接AF,若AF=10,求正方形ABCD的面积;
(2)如图2,把△ADE绕点D顺时针旋转90°得到△CDF,连接AF,取AF的中点为M,连接DM,求证:4DM2+AE2=2DF2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(﹣1,0).
(1)请直接写出点B、C的坐标:B( )、C( );并求经过A、B、C三点的抛物线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(1)中的抛物线交于点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形?若存在,请写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CA=CB,点O在△ABC的内部,⊙O经过B,C两点,交AB于点D,连接CO并延长交AB于点G,以GD,GC为邻边作GDEC.
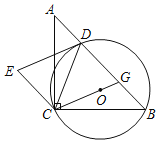
(1)判断DE与⊙O的位置关系,并说明理由.
(2)若点B是![]() 的中点,⊙O的半径为2,求
的中点,⊙O的半径为2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.
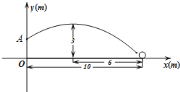
![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com