
【题目】如图1,直线y=x+1与抛物线![]() 相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.
相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.
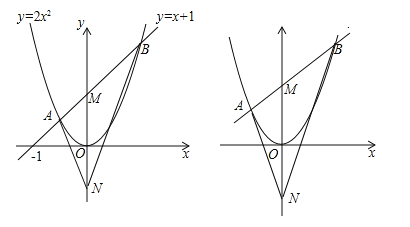
(1)①求A、B的坐标;②求证:∠ANM=∠BNM;
(2)如图2,将题中直线y=x+1变为y=kx+b(b>0),抛物线![]() 变为
变为![]() (a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
(a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
【答案】(1)①A(![]() ,
,![]() ),B( 1,2);②证明见解析;(2)成立,理由见解析.
),B( 1,2);②证明见解析;(2)成立,理由见解析.
【解析】
(1)①联立直线和抛物线解析式可求得A、B两点的坐标;②过A作AC⊥y轴于C,过B作BD⊥y轴于D,可分别求得∠ANM和∠BNM的正切值,可证得结论;
(2)当k=0时,由对称性可得出结论;当k≠0时,过A作AE⊥y轴于E,过B作BF⊥y轴于F,设A(![]() ,
,![]() )、B(
)、B(![]() ,
,![]() ),联立直线和抛物线解析式,消去y,利用根与系数的关系,可求得
),联立直线和抛物线解析式,消去y,利用根与系数的关系,可求得![]() ,则可证明Rt△AEN∽Rt△BFN,可得出结论.
,则可证明Rt△AEN∽Rt△BFN,可得出结论.
解:(1)①由已知得![]() ,解得
,解得![]() 或x=1,当
或x=1,当![]() 时,y=
时,y=![]() ,当x=1时,y=2,∴A、B两点的坐标分别为(
,当x=1时,y=2,∴A、B两点的坐标分别为(![]() ,
,![]() ),( 1,2);
),( 1,2);
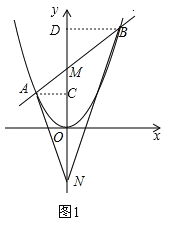
②如图1,过A作AC⊥y轴于C,过B作BD⊥y轴于D,由①及已知有A(![]() ,
,![]() ),B( 1,2),且OM=ON=1,∴tan∠ANM=
),B( 1,2),且OM=ON=1,∴tan∠ANM=![]() =
=![]() =
=![]() ,tan∠BNM=
,tan∠BNM=![]() =
=![]() =
=![]() ,∴tan∠ANM=tan∠BNM,∴∠ANM=∠BNM;
,∴tan∠ANM=tan∠BNM,∴∠ANM=∠BNM;
(2)∠ANM=∠BNM成立,①当k=0,△ABN是关于y轴的轴对称图形,∴∠ANM=∠BNM;
②当k≠0,根据题意得:OM=ON=b,设A(![]() ,
,![]() )、B(
)、B(![]() ,
,![]() ).
).
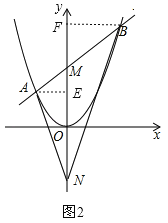
如图2,过A作AE⊥y轴于E,过B作BF⊥y轴于F,由题意可知:ax2=kx+b,即ax2﹣kx﹣b=0,∴![]() ,
,![]() ,∵
,∵![]()
![]()
=![]() =
=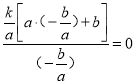 ,
,
∴![]() ,
,
∴Rt△AEN∽Rt△BFN,
∴∠ANM=∠BNM.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为()cm2.
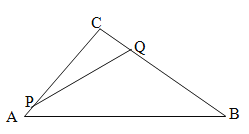
A. 19 B. 16 C. 15 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
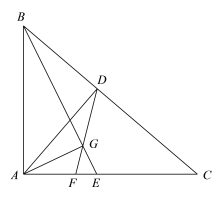
【题目】如图,△ABC中,D是BC上一点,E是AC上一点,点G在BE上,联结DG并延长交AE于点F,∠BGD=∠BAD=∠C.
(1)求证:![]() ;
;
(2)如果∠BAC=90°,求证:AG⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3700元购进第二批仙桃,所购件数是第一批的![]() 倍,但进价比第一批每件多了5元.
倍,但进价比第一批每件多了5元.
(1)第一批仙桃每件进价是多少元?
(2)老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
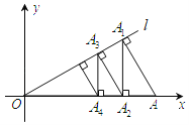
【题目】 如图,过点A(2,0)作直线l:y=![]() 的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:AA1,A1A2,A2A3,…,则线段A2018A2019的长为______.
的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:AA1,A1A2,A2A3,…,则线段A2018A2019的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸和小明旱晨同时从家出发,以各自的速度匀速步行上班和上学,爸爸前往位于家正东方的公司,小明前往位于家正西方的学校,爸爸到达公司后发现小明的数学作业在自己的公文包里,于是立即跑步去追小明,终于在途中追上了小明把作业给了他,然后再以先前的速度步行再回公司(途中给作业的时间忽略不计). 结果爸爸回到公司的时间比小明到达学校的时间多用了8分钟. 如图是两人之间的距离y(米)与他们从家出发的时间x(分钟)的函数关系图,则小明家与学校相距_____米.
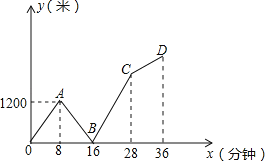
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校初三学生每周平均阅读时间的情况,随机抽查了该校初三m名学生,对其每周平均课外阅读时间进行统计,绘制了条形统计图和扇形统计图.
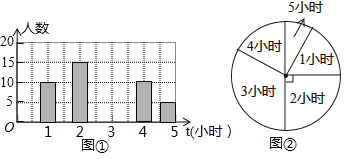
根据以上信息回答下列问题:
(1)求m的值;
(2)求扇形统计图中阅读时间为3小时的扇形圆心角的度数;
(3)求出这组数据的平均数.(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com