
【题目】如图,抛物线y = x2+bx+c过点A (-1,2),且关于y轴对称,点C与点B(a,0)(a>1)关于原点对称,直线AC交抛物线于点D.
(1)求此抛物线的解析式;
(2)连接OA,BD,当OA//BD时,求a的值;
(3)若直线AC交抛物线![]() 于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.
于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)y=2x+4.
;(3)y=2x+4.
【解析】
(1)根据抛物线的对称轴可得b的值,代入A点的坐标即可求出c的值;
(2)根据OA//BD和A点坐标可求出D点坐标,然后代入函数解析式即可解答;
(3)设A(xA,yA),D(xD,yD),E(xE,yE),F(xF,yF),根据EA=DF可得,xA-xE=xF-xD,xA+xD=xF+xE,根据A(-1,2),C(-a,0)求出直线AC解析式为![]() ,然后与两个抛物线联立可得关于a的方程,解出a的值然后即可求出直线AC的解析式.
,然后与两个抛物线联立可得关于a的方程,解出a的值然后即可求出直线AC的解析式.
(1)∵抛物线关于y轴对称,
∴b=0,
把A (-1,2),b=0代入y = x2+bx+c,得c=1,
∴抛物线解析式为:![]() ;
;
(2)∵B、C关于原点对称,B(a,0)
∴C(-a,0),
∵OA∥BD,
∴点A是CD中点,
∵A (-1,2),
∴D (a-2,4),
把D (a-2,4)代入![]() ,得
,得![]() ,
,
解得:![]() ,
,
∵a>1,
∴![]() ;
;
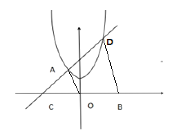
(3)设A(xA,yA),D(xD,yD),E(xE,yE),F(xF,yF),
∵EA=DF,∴xA-xE=xF-xD ∴xA+xD=xF+xE,
把A(-1,2),C(-a,0)代入求得直线AC解析式为:![]() ,
,
联立,得: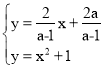 ,
,
∴![]() ,
,
∴xA+xD=![]() ,
,
联立,得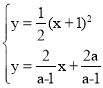 ,
,
∴![]() ,
,
∴xF+xE=![]() ,
,
∴![]() =
=![]() ,
,
解得:a=2,经检验a=2是原方程的解且符合题意,
∴直线AC解析式为:y=![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
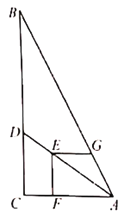
A.3.6B.4C.4.8D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课时,王明、赵丽、高洁、李虎四位同学围成一圈玩传球游戏(假设传球的对象都是随机的),若开始时球在王明手中.
(1)经过一次传球后,球在高洁手里的概率是多少?
(2)求:经过两次传球后,球又回到王明手中的概率(用树状图或列表法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面内,抛物线经过原点![]() 、点
、点![]() ,又与
,又与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 作
作![]() ,与抛物线交于点
,与抛物线交于点![]() ,且点
,且点![]() 在第一象限内.
在第一象限内.
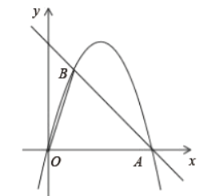
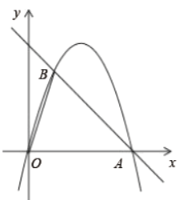
备用图
(1)求抛物线的表达式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)过点![]() 作
作![]() 轴,分别交直线
轴,分别交直线![]() 、
、![]() 轴于点
轴于点![]() 、
、![]() ,若
,若![]() 的面积等于
的面积等于![]() 的面积的
的面积的![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A'B'C'D',此时点B'恰好落在边AD上.
(1)画出旋转后的图形;
(2)连接B'B,若∠AB'B=75°,求旋转角及AB长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
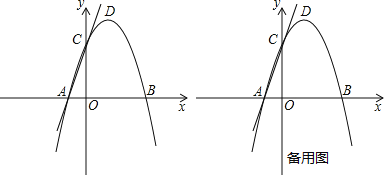
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,点
,点![]() 、
、![]() 的横坐标是一元二次方程
的横坐标是一元二次方程![]() 的两根(
的两根(![]() ),直线
),直线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
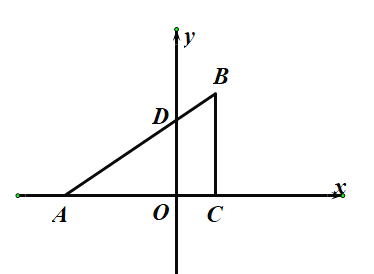
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)在![]() 轴上找一点
轴上找一点![]() ,连接
,连接![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似(不包括全等),并求点
相似(不包括全等),并求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,连接
上的动点,连接![]() ,点
,点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,以每秒1个单位长度的速度运动,当点
同时出发,以每秒1个单位长度的速度运动,当点![]() 到达点
到达点![]() 时,两点停止运动,设运动时间为
时,两点停止运动,设运动时间为![]() 秒,请直接写出几秒时以点
秒,请直接写出几秒时以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级从甲、乙两位同学中选派一人参加知识竞赛,老师对他们的五次模拟成绩(单位:分)进行了整理,并计算出甲成绩的平均数是80分,甲、乙成绩的方差分别是320,40,但绘制的统计图表尚不完整.
甲、乙两人模拟成绩统计表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲成绩 | 90 | 100 | 90 | 50 |
|
乙成绩 | 80 | 70 | 80 | 90 | 80 |
甲、乙两人模拟成绩折线图
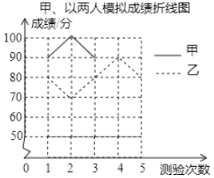
根据以上信息,请你解答下列问题:
(1)![]()
(2)请完成图中表示甲成绩变化情况的折线;
(3)求乙成绩的平均数;
(4)从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com