
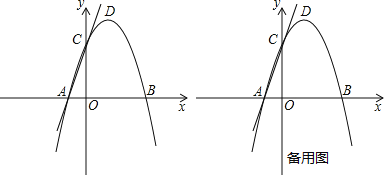
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+2x+c��x�ύ��A����1��0��B��3��0�����㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣮
��1���������ߵĽ���ʽ��ֱ��AC�Ľ���ʽ��
��2������y������һ��M��ʹ��BDM���ܳ���С�������M�����ꣻ
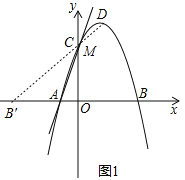
��3����̽�����ڒ��������Ƿ���ڵ�P��ʹ�Ե�A��P��CΪ���㣬ACΪֱ�DZߵ���������ֱ�������Σ������ڣ���������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1�������߽���ʽΪy=��x2+2x+3��ֱ��AC�Ľ���ʽΪy=3x+3����2����M������Ϊ��0��3����
��3�����������ĵ�P������Ϊ��![]() ��
��![]() ����
����![]() ����
����![]() ����
����
����������1���轻��ʽy=a��x+1����x-3����չ���õ�-2a=2��Ȼ�����a���ɵõ������߽���ʽ����ȷ��C��0��3����Ȼ�����ô���ϵ������ֱ��AC�Ľ���ʽ��
��2�����ö��κ���������ȷ��D������Ϊ��1��4������B�����y��ĶԳƵ�B��������DB����y����M����ͼ1����B�䣨-3��0������������֮���߶���̿��жϴ�ʱMB+MD��ֵ��С�����ʱ��BDM���ܳ���С��Ȼ�����ֱ��DB���Ľ���ʽ���ɵõ���M�����ꣻ
��3������C��AC�Ĵ��߽�����������һ��P����ͼ2��������ֱ�ߴ�ֱһ����ϵ����Ϊ��������ֱ��PC�Ľ���ʽΪy=-![]() x+b����C������������b�õ�ֱ��PC�Ľ���ʽΪy=-
x+b����C������������b�õ�ֱ��PC�Ľ���ʽΪy=-![]() x+3���ٽⷽ����
x+3���ٽⷽ����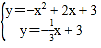 �ô�ʱP�����ꣻ������A��AC�Ĵ��߽�����������һ��Pʱ������ͬ���ķ����������ʱP�����꣮
�ô�ʱP�����ꣻ������A��AC�Ĵ��߽�����������һ��Pʱ������ͬ���ķ����������ʱP�����꣮
��1���������߽���ʽΪy=a��x+1����x��3����
��y=ax2��2ax��3a��
����2a=2�����a=��1��
�������߽���ʽΪy=��x2+2x+3��
��x=0ʱ��y=��x2+2x+3=3����C��0��3����
��ֱ��AC�Ľ���ʽΪy=px+q��
��A����1��0����C��0��3�������![]() �����
�����![]() ��
��
��ֱ��AC�Ľ���ʽΪy=3x+3��
��2����y=��x2+2x+3=����x��1��2+4��
�ඥ��D������Ϊ��1��4����
��B�����y��ĶԳƵ�B��������DB����y����M����ͼ1����B�䣨��3��0����
��MB=MB�䣬
��MB+MD=MB��+MD=DB������ʱMB+MD��ֵ��С��
��BD��ֵ���䣬
���ʱ��BDM���ܳ���С��
��ֱ��DB���Ľ���ʽΪy=x+3��
��x=0ʱ��y=x+3=3��
���M��������0��3����
��3�����ڣ�
����C��AC�Ĵ��߽�����������һ��P����ͼ2��
��ֱ��AC�Ľ���ʽΪy=3x+3��
��ֱ��PC�Ľ���ʽ����Ϊy=��![]() x+b��
x+b��
��C��0��3�������b=3��
��ֱ��PC�Ľ���ʽΪy=��![]() x+3��
x+3��
�ⷽ����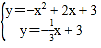 �����
�����![]() ��
��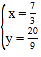 �����ʱP������Ϊ��
�����ʱP������Ϊ��![]() ��
��![]() ����
����
����A��AC�Ĵ��߽�����������һ��P��ֱ��PC�Ľ���ʽ����Ϊy=��![]() x+b��
x+b��
��A����1��0�������![]() +b=0�����b=��
+b=0�����b=��![]() ��
��
��ֱ��PC�Ľ���ʽΪy=��![]() x��
x��![]() ��
��
�ⷽ����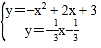 �����
�����![]() ��
��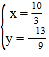 �����ʱP������Ϊ��
�����ʱP������Ϊ��![]() ����
����![]() ��.
��.
�������������������ĵ�P������Ϊ��![]() ��
��![]() ������
������![]() ����
����![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
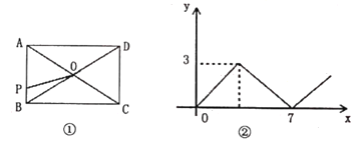
����Ŀ����ͼ�٣��ھ���ABCD�У�AB<AD���Խ���AC��BD�ཻ�ڵ�O������P�ɵ�A��������AB-BC��CD���D�˶����P���˶�·��Ϊx����AOP�����Ϊy��y��x�ĺ�����ϵͼ����ͼ����Сʾ����AD�ij�Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
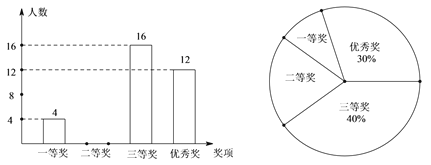
����Ŀ��ij��ѧ��ȫУѧ���п�չ�������������ǵļ���Ϊ����Ļ������ı�������ѡ��һ���������Ƚ������㽱�����ݽ����������Ƴ���ͼ��ʾ��������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
��1����У������������������ͳ��ͼ����������
��2����������ͳ��ͼ�б�ʾ�����Ƚ��� �����ε�Բ�ĽǵĶ�����
��3�����һ�Ƚ���4��ѧ������3��1Ů���ִ���������ѡ��2��ѧ���μӰ佱��������б�����״ͼ�ķ�����ѡ����2��ѧ��ǡ����1��1Ů�ĸ��ʩq
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ȱ���ABC�ı߳�Ϊ8����ABΪֱ����Բ��BC�ڵ�F����CΪԲ�ģ�CF��Ϊ�뾶��ͼ��D�ǡ�C��һ���㣬EΪBD���е㣬��AE���ʱ��BD�ij�Ϊ��������

A. ![]() B.
B. ![]() C.
C. ![]() D. 12
D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y = x2+bx+c����A (-1��2)���ҹ���y��Գƣ���C���B(a��0)(a��1)����ԭ��Գƣ�ֱ��AC���������ڵ�D��
��1����������ߵĽ���ʽ��
��2������OA��BD����OA//BDʱ����a��ֵ��
��3����ֱ��AC��������![]() ��E��F����(��E�ڵ�F�����)����EA=DF����ֱ��AC�Ľ���ʽ��
��E��F����(��E�ڵ�F�����)����EA=DF����ֱ��AC�Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���![]()
��1����֤������kȡʲôʵ��ֵ�������������ʵ������
��2��������������ABC��һ�߳�Ϊ![]() �������ߵij�b��cǡ����������̵������������ABC���ܳ���
�������ߵij�b��cǡ����������̵������������ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Ļ���Ʒ�̵깺�����������200�������ۺ��ۼ����±�ȫ�������������2600Ԫ��
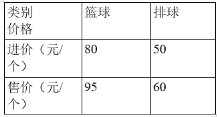
��1�����̵깺���������������ٸ���
��2������ʦ��Ԫ�������쵽�������Ļ���Ʒ�̵�ΪѧУ���������������ɸ������������ˣ����̵���������ʽ����л���100Ԫ����ʦ���ļ��ֹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
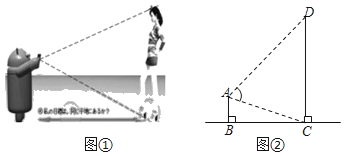
����Ŀ�������ֻ������װ��һ�����������SmartMeasure���Ϳ��Բ�����ߡ����Ⱥ�����ȣ���ͼ�����������ֻ�����ͷ����Ļ�Ƕ��Ų��������ٶ�ͷ�����������ɲ���������ĸ߶ȣ�����ѧԭ����ͼ����ʾ��������AB�뱻������CD����ֱ�ڵ���BC�����ֻ���ʾAC��1m��AD��1��8m����CAD��60�㣬���ʱCD�ĸߣ�������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
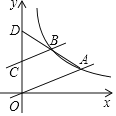
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��˫����
��˫����![]() ���ڵ�A������
���ڵ�A������![]() ��AO��ƽ���߽�˫�����ڵ�B������AB���ӳ���y�ύ�ڵ�
��AO��ƽ���߽�˫�����ڵ�B������AB���ӳ���y�ύ�ڵ�![]() ����k��ֵΪ______��
����k��ֵΪ______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com