
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
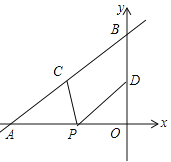
A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
根据以上信息,解答下列问题:
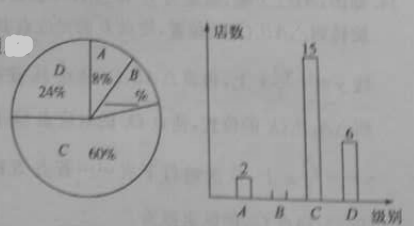
(1)本次评估随机抽取了多少家商业连锁店?
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从![]() 、
、![]() 两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是
两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是![]() 等级的概率.
等级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论: ①EG=FG;②∠ABG=60°;③AE=1;④△BEF是等边三角形;其中正确结论的序号是 . 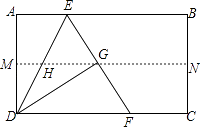
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
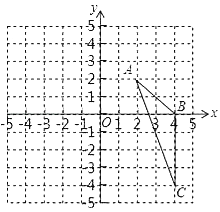
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE. 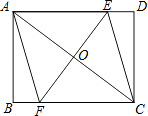
(1)求证:四边形AFCE是菱形;
(2)若AB=3,AD=4,求菱形AFCE的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com