
 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发去乙地.如图,线段OA表示货车离开甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离开甲地的距离y(千米)与时间x(小时)之间的函数关系.
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发去乙地.如图,线段OA表示货车离开甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离开甲地的距离y(千米)与时间x(小时)之间的函数关系.分析 (1)根据图形中点的坐标的意义,再结合速度=路程÷时间,即可得出结论;
(2)设出解析式,由待定系数法即可求出解析式;
(3)由(2)的结论,令y1=y2算出相遇时间,在由路程=时间×速度即可得出结论;
(4)轿车到乙地时,货车离乙地还有30千米,由时间=路程÷两车速度和,即可得知结论.
解答 解:(1)货车的速度为300÷5=60(千米/小时);
轿车在2.5小时后的速度是(300-80)÷(4.5-2.5)=110(千米/小时).
故答案为:60;110.
(2)设线段OA对应的函数解析式为y1=k1x,线段CD对应的函数解析式为y2=k2+b.
结合图形可知:300=5k1,解得:k1=60.
故线段OA对应的函数解析式为y1=60x(0≤x≤5).
由C点(2.5,80)和D点(4.5,300)在线段CD上,可知:
$\left\{\begin{array}{l}{80=2.5{k}_{2}+b}\\{300=4.5{k}_{2}+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{2}=110}\\{b=-195}\end{array}\right.$.
故线段CD对应的函数解析式为y2=110x-195(2.5≤x≤4.5).
(3)令y1=y2,则有60x=110x-195,
解得:x=3.9.
此时相距乙地300-60×3.9=66(千米).
答:货车出发3.9小时后与轿车相遇,相遇时两车距离乙地还有66千米.
(4)当轿车到达乙地时,货车离乙地的距离为:300-4.5×60=30(千米),
二者在次相遇还需要的时间为30÷(60+110)=$\frac{3}{17}$(小时),
此时货车从甲地出发时间为4.5+$\frac{3}{17}$=$\frac{159}{34}$=4$\frac{23}{34}$(小时).
答:货车从甲地出发后4$\frac{23}{34}$小时再次与轿车相遇.
点评 本题考查了一次函数的相遇问题以及由待定系数法求函数解析式,解题的关键是:(1)速度=路程÷时间;(2)利用待定系数法求解析式;(3)令y1=y2,解关于x的一元一次方程;(4)结合行程得出结论.本题属于中档题,难度不大,但比较繁琐,运算过程中要务必细心,这样才能拿到满分.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:初中数学 来源: 题型:选择题
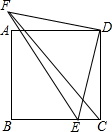 如图,在正方形ABCD中,E是BC上的动点(不与点B、C重合),连接DE,过点D作FD⊥ED于点D,并使FD=ED,连接CF,EF,下列角的大小比较中,一定正确的是( )
如图,在正方形ABCD中,E是BC上的动点(不与点B、C重合),连接DE,过点D作FD⊥ED于点D,并使FD=ED,连接CF,EF,下列角的大小比较中,一定正确的是( )| A. | ∠ADF>∠CDE | B. | ∠DCF>∠DFC | C. | ∠DFC>∠ADF | D. | ∠DEC>∠BEF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
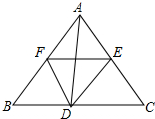 在△ABC中,D,E,F分别是BC、AB、AC的中点.
在△ABC中,D,E,F分别是BC、AB、AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com