练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】阅读下面文字并填空：数学课上张老师出了这样一道题：“如图，在中，，是中线，点为的中点，连接.求证：”

    张老师给出了如下简要“要证，就是要证线段的倍分问题，所以有两个思路，思路一：找，故取的中点，连接，只要证即可.这就将证明线段倍分问题______为证明线段相等问题，只要证出______，则结论成立.思路二：变为，因为需要找到，于是延长至点，使，只要证______即可.连接，若证出____________则结论成立.”你认为在现阶段可以用思路______来完成这个证明.

    【答案】转化；；, , ；二

    证明过程见详解

    【解析】

    按照张老师的思路即可填出答案，利用全等三角形的判定及性质来证明，从而有，从而结论可证.所以思路二可以证明.

    转化；；, , ；二

    证明：延长至点，使

    ∵点为的中点

    ∴

    在和中，

    ∵，是中线

    在和中，

    ∴

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形中，已知，，对角线平分，，，则边的长度为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品的进价为每件元，现在的售价为每件元，每星期可卖出件．市场调查反映：如果每件售价每涨元（售价每件不能高于元），那么每星期少卖件．设每件售价为元（为非负整数），则若要使每星期的利润最大且每星期的销量较大，应为多少元？( )

    A. 41 B. 42 C. 42.5 D. 43

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年五、六月份，我省各地、市普遭暴雨袭击，水位猛涨．某市抗洪抢险救援队伍在处接到报告：有受灾群众被困于一座遭水淹的楼顶处，情况危急！救援队伍在处测得在的北偏东的方向上（如图所示），队伍决定分成两组：第一组马上下水游向处救人，同时第二组从陆地往正东方向奔跑米到达处，再从处下水游向处救人，已知在的北偏东的方向上，且救援人员在水中游进的速度均为米/秒．在陆地上奔跑的速度为米/秒，试问哪组救援队先到处？请说明理由．（参考数据）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：

    使用次数

    0

    1

    2

    3

    4

    5(含5次以上)

    累计车费

    0

    0.5

    0.9

    1.5

    同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：

    使用次数

    0

    1

    2

    3

    4

    5

    人数

    5

    15

    10

    30

    25

    15

    （Ⅰ）写出的值；

    （Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利? 说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，一次函数y=﹣2x+8的图象与x轴，y轴分别交于点A，点C，过点A作AB⊥x轴，垂足为点A，过点C作CB⊥y轴，垂足为点C，两条垂线相交于点B．

    （1）线段AB，BC，AC的长分别为AB=　 　，BC=　 　，AC=　 　；

    （2）折叠图1中的△ABC，使点A与点C重合，再将折叠后的图形展开，折痕DE交AB于点D，交AC于点E，连接CD，如图2．

    请从下列A、B两题中任选一题作答，我选择　 　题．

    A：①求线段AD的长；

    ②在y轴上，是否存在点P，使得△APD为等腰三角形？若存在，请直接写出符合条件的所有点P的坐标；若不存在，请说明理由．

    B：①求线段DE的长；

    ②在坐标平面内，是否存在点P（除点B外），使得以点A，P，C为顶点的三角形与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等边△ABC的边长为12，D是AB上的动点，过D作DE⊥BC于点E，过E作EF⊥AC于点F，过F作FG⊥AB于点G.当G与D重合时，AD的长是（ ）

    A.9B.8C.4D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】李大爷要围成一个矩形菜园，菜园的一边利用足够长的墙，用篱笆围成的另外三边总长应恰好为24米．要围成的菜园是如图所示的矩形ABCD．设BC边的长为x米，AB边的长为y米，则y与x之间的函数关系式是( )

    A. y=－2x+24(0<x<12) B. y=－x＋12(0<x<24)

    C. y=2x－24(0<x<12) D. y=x－12(0<x<24)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

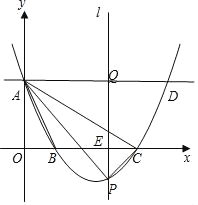
    【题目】如图，在平面直角坐标系中，抛物线y=x2+bx+c与y轴的交于点A（0，3），与x轴的交于点B和C，点B的横坐标为2．点A关于抛物线对称轴对称的点为点D，在x轴上有一动点E（t，0），过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q．

    （1）求抛物线的解析式；

    （2）当点P在线段AC的下方时，求△APC面积的最大值；

    （3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似．若存在，求出此时t的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案