
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c与y轴的交于点A(0,3),与x轴的交于点B和C,点B的横坐标为2.点A关于抛物线对称轴对称的点为点D,在x轴上有一动点E(t,0),过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q.
x2+bx+c与y轴的交于点A(0,3),与x轴的交于点B和C,点B的横坐标为2.点A关于抛物线对称轴对称的点为点D,在x轴上有一动点E(t,0),过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当点P在线段AC的下方时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似.若存在,求出此时t的值;若不存在,请说明理由.
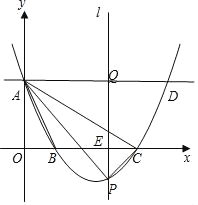
【答案】(1)抛物线的解析式为y=![]() x2﹣2x+3;(2)当t=3时,△APC的面积取最大值,最大值为
x2﹣2x+3;(2)当t=3时,△APC的面积取最大值,最大值为![]() ;(3)当t>2时,存在点P,使以A、P、Q为顶点的三角形与△AOB相似,此时t的值为
;(3)当t>2时,存在点P,使以A、P、Q为顶点的三角形与△AOB相似,此时t的值为![]() 或
或![]() 或14.
或14.
【解析】
(1)由点A、B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,由点A、C的坐标利用待定系数法可求出直线AC的解析式,设直线l与直线AC的交点为F,则点F的坐标为(t,﹣![]() t+3).结合点P的坐标即可得出PF的值,由S△APC=S△APF+S△CPF可得出S△APC=﹣
t+3).结合点P的坐标即可得出PF的值,由S△APC=S△APF+S△CPF可得出S△APC=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,再利用二次函数的性质即可解决最值问题;
,再利用二次函数的性质即可解决最值问题;
(3)由∠AOB=∠AQP=90°,可分△AOB∽△AQP和△AOB∽△PQA两种情况考虑,利用相似三角形的性质可得出关于t的方程,解之即可得出结论.
(1)将A(0,3)、B(2,0)代入y=![]() x2+bx+c,得:
x2+bx+c,得:
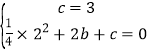 ,解得:
,解得:![]() ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x2﹣2x+3.
x2﹣2x+3.
(2)当y=0时,有![]() x2﹣2x+3=0,解得:x1=2,x2=6,∴点C的坐标为(6,0).
x2﹣2x+3=0,解得:x1=2,x2=6,∴点C的坐标为(6,0).
设直线AC的解析式为y=mx+n(m≠0),将A(0,3)、C(6,0)代入y=mx+n,得:
![]() ,解得:
,解得: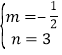 ,∴直线AC的解析式为y=﹣
,∴直线AC的解析式为y=﹣![]() x+3.
x+3.
设直线l与直线AC的交点为F,如图1所示,则点F的坐标为(t,﹣![]() t+3).
t+3).
∵点P的坐标为(t,![]() t2﹣2t+3),∴PF=﹣
t2﹣2t+3),∴PF=﹣![]() t+3﹣(
t+3﹣(![]() t2﹣2t+3)=﹣
t2﹣2t+3)=﹣![]() t2+
t2+![]() t,∴S△APC=S△APF+S△CPF=
t,∴S△APC=S△APF+S△CPF=![]() OEPF+
OEPF+![]() CEPF=
CEPF=![]() OCPF=
OCPF=![]() ×6×(﹣
×6×(﹣![]() t2+
t2+![]() t)=﹣
t)=﹣![]() (t﹣3)2+
(t﹣3)2+![]() .
.
∵a=﹣![]() <0,当t=3时,△APC的面积取最大值,最大值为
<0,当t=3时,△APC的面积取最大值,最大值为![]() .
.
(3)假设存在.
∵∠AOB=∠AQP=90°,∴分△AOB∽△AQP和△AOB∽△PQA两种情况考虑.
∵A(0,3),B(2,0),Q(t,3),P(t,![]() t2﹣2t+3),∴AO=3,BO=2,AQ=t,PQ=|
t2﹣2t+3),∴AO=3,BO=2,AQ=t,PQ=|![]() t2﹣2t|.
t2﹣2t|.
①当△AOB∽△AQP时,有![]() =
=![]() ,即
,即![]() =
=![]() ,解得:t1=0(舍去),t2=
,解得:t1=0(舍去),t2=![]() ,t3=
,t3=![]() ,经检验,t2=
,经检验,t2=![]() 、t3=
、t3=![]() 是所列分式方程的解;
是所列分式方程的解;
②当△AOB∽△PQA时,有![]() =
=![]() ,即
,即![]() =
=![]() ,解得:t4=0(舍去),t5=2(舍去),t6=14,经检验,t6=14是所列分式方程的解.
,解得:t4=0(舍去),t5=2(舍去),t6=14,经检验,t6=14是所列分式方程的解.
综上所述:当t>2时,存在点P,使以A、P、Q为顶点的三角形与△AOB相似,此时t的值为![]() 或
或![]() 或14.
或14.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】阅读下面文字并填空:数学课上张老师出了这样一道题:“如图,在![]() 中,
中,![]() ,
,![]() 是中线,点
是中线,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .求证:
.求证:![]() ”
”

张老师给出了如下简要“要证![]() ,就是要证线段的倍分问题,所以有两个思路,思路一:找
,就是要证线段的倍分问题,所以有两个思路,思路一:找![]() ,故取
,故取![]() 的中点
的中点![]() ,连接
,连接![]() ,只要证
,只要证![]() 即可.这就将证明线段倍分问题______为证明线段相等问题,只要证出______,则结论成立.思路二:变
即可.这就将证明线段倍分问题______为证明线段相等问题,只要证出______,则结论成立.思路二:变![]() 为
为![]() ,因为需要找到
,因为需要找到![]() ,于是延长
,于是延长![]() 至点
至点![]() ,使
,使![]() ,只要证______即可.连接
,只要证______即可.连接![]() ,若证出______
,若证出______![]() ______则结论成立.”你认为在现阶段可以用思路______来完成这个证明.
______则结论成立.”你认为在现阶段可以用思路______来完成这个证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家八纵八横高铁网络规划中“京昆通道”的重要组成部分──西成高铁于2017年12月6日开通运营,西安至成都列车运行时间由14小时缩短为3.5小时.张明和王强相约从成都坐高铁到西安旅游.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
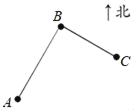
A. 6000米 B. 5000米 C. 4000米 D. 2000米
查看答案和解析>>
科目:初中数学 来源: 题型:
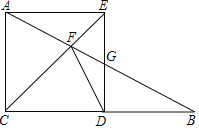
【题目】在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
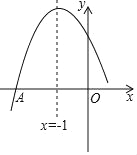
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=﹣1,与x轴的一个交点是A(﹣3,0)其图象的一部分如图所示,对于下列说法:①2a=b;②abc>0,③若点B(﹣2,y1),C(﹣![]() ,y2)是图象上两点,则y1<y2;④图象与x轴的另一个交点的坐标为(1,0).其中正确的是_____(把正确说法的序号都填上)
,y2)是图象上两点,则y1<y2;④图象与x轴的另一个交点的坐标为(1,0).其中正确的是_____(把正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | |
A村(元/辆) | B村(元/辆) | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D是矩形的四个顶点,AB=16cm,BC=6cm,动点P从点A出发,以3cm/s的速度向点B运动,直到点B为止;动点Q同时从点C出发,以2cm/s的速度向点D运动,当时间为_______时,点P和点Q之间的距离是10cm

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com