
【题目】如图,A、B、C、D是矩形的四个顶点,AB=16cm,BC=6cm,动点P从点A出发,以3cm/s的速度向点B运动,直到点B为止;动点Q同时从点C出发,以2cm/s的速度向点D运动,当时间为_______时,点P和点Q之间的距离是10cm

【答案】![]() 或
或![]()
【解析】
求出当PQ∥BC即BP=CQ时的时间,从而确定t的范围并进行分类讨论,分两类:①当0≤t≤3.2;②当3.2<t≤8,表示出对应线段的长度,结合勾股定理分别列出方程,解方程并对t进行取舍即可.
设时间为t,
当PQ∥BC时,BP=CQ,
16﹣3t=2t,解得t=3.2s,
点P从A点运动至B点的时间为:16÷3=![]() s,
s,
点Q从C点运动至D点的时间为:16÷2=8s,
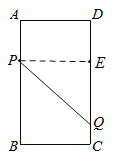
①当0≤t≤3.2时,如图,作PE⊥CD交CD于点E,
由题意得AP=DE=3t,CQ=2t,PE=6,
∴EQ=16﹣5t,
∵PE2+EQ2=PQ2,
∴62+(16﹣5t)2=102,
解得t1=![]() ,t2=
,t2=![]() (舍去);
(舍去);
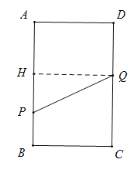
②当3.2<t≤8时,如图作QH⊥AB交AB于点H,
由题意得AP=3t,CQ=2t, DH=6,
∴AH=DQ=16﹣2t,
∴PH=5t﹣16,
∵PH2+HQ2=PQ2,
∴(5t﹣16)2+62=102,
解得t1=![]() (舍去),t2=
(舍去),t2=![]() ;
;
∴t=![]() 或
或![]() .
.
故答案为![]() 或
或![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
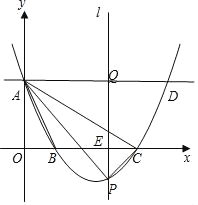
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c与y轴的交于点A(0,3),与x轴的交于点B和C,点B的横坐标为2.点A关于抛物线对称轴对称的点为点D,在x轴上有一动点E(t,0),过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q.
x2+bx+c与y轴的交于点A(0,3),与x轴的交于点B和C,点B的横坐标为2.点A关于抛物线对称轴对称的点为点D,在x轴上有一动点E(t,0),过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当点P在线段AC的下方时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似.若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气持续笼罩某地区,口罩市场出现热卖.某商店用8000元购进甲、乙两种口罩,销售完后共获利2800元,其进价和售价如下表:
甲种口罩 | 乙种口罩 | |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该商店购进甲、乙两种口罩各多少袋?
(2)该商店第二次仍以原价购进甲、乙两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍,甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,则乙种口罩最低售价为每袋多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ΔABC中,AB=AC,若将ΔABC绕点C顺时针180得到ΔFEC。

(1)试猜想AE与BF有何关系,并说明理由;
(2)若ΔABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,2),B(-4,-3),C(-1,-1)。

(1)写出△ABC关于x轴对称的△A1B1C1 的各顶点坐标;
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)求△A2B2C2的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式2a(b+c)-3(b+c)的结果是______.
【答案】(b+c)(2a-3)
【解析】解析:2a(b+c)-3(b+c)=(b+c)(2a-3).
点睛:因式分解的方法:(1)提取公因式法.ma+mb+mc=m(a+b+c).
(2)公式法:完全平方公式,平方差公式.
(3)十字相乘法.
因式分解的时候,要注意整体换元法的灵活应用,训练将一个式子看做一个整体,利用上述方法因式分解的能力.
【题型】填空题
【结束】
17
【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究与应用:

(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式 (用式子表达)
(4)运用你所得到的公式计算:10.3×9.7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别以
分别以![]() 、
、![]() 的速度从点
的速度从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 向点
向点![]() 移动.
移动.

![]() 若点
若点![]() 从点
从点![]() 移动到点
移动到点![]() 停止,点
停止,点![]() 随点
随点![]() 的停止而停止移动,点
的停止而停止移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,问经过多长时间
同时出发,问经过多长时间![]() 、
、![]() 两点之间的距离是
两点之间的距离是![]() ?
?
![]() 若点
若点![]() 沿着
沿着![]() 移动,点
移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 移动到点
移动到点![]() 停止时,点
停止时,点![]() 随点
随点![]() 的停止而停止移动,试探求经过多长时间
的停止而停止移动,试探求经过多长时间![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某校有一块菱形空地ABCD,∠A=60°,AB=40m,现计划在内部修建一个四个顶点分别落在菱形四条边上的矩形鱼池EFGH,其余部分种花草,园林公司修建鱼池,草坪的造价为y(元)与修建面积s(m2)之间的函数关系如图2所示,设AE为x米.

(1)填空:ED= m,EH= m,(用含x的代数式表示);
(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)
(2)若矩形鱼池EFGH的面积是300![]() m2,求EF的长度;
m2,求EF的长度;
(3)EF的长度为多少时,修建的鱼池和草坪的总造价最低,最低造价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com