
【题目】如图,在ΔABC中,AB=AC,若将ΔABC绕点C顺时针180得到ΔFEC。

(1)试猜想AE与BF有何关系,并说明理由;
(2)若ΔABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由。
【答案】(1)AE=BF且AE∥BF (2)12CM (3)∠ACB=60o
【解析】
(1)根据AB=AC,△FEC是由△ABC绕点C顺时针旋转180°产生的,可得到四边形ABFE是平行四边形,既而可得AE∥BF且AE=BF;
(2)由于等底同高的两个三角形面积相等,可得图中四个三角形的面积相等,所以S四边形ABFE=4×S△ABC,可得答案;
(3)当∠ACB=60°时,AB=AC=BC,可得AF=BE,即四边形ABFE是矩形.
解:(1)AE∥BF,AE=BF.
理由如下:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形,
∴AE∥BF,AE=BF;
(2)∵BC=CE,
∴ S△ABC=S△ACE;
∵AC=CF,
∴S△ABC=S△FBC,S△ACE=S△FCE;
∴ S四边形ABFE=4×S△ABC=12cm2;
(3)当∠ACB=60°时,四边形ABFE是矩形.理由如下:
∵∠ACB=60°时,AB=AC,
∴AB=AC=BC,
又∵AC=CF,BC=CE,
∴AF=BE,
∴平行四边形ABFE是矩形.


科目:初中数学 来源: 题型:
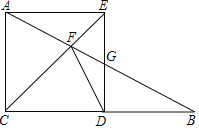
【题目】在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC在平面直角坐标系内(0为坐标原点),点A在x轴上,点C在y轴上,点B的坐标分别为(-2,2![]() ),点E是BC的中点,点H在OA上,且AH=
),点E是BC的中点,点H在OA上,且AH=![]() ,过点H且平行于y轴的HG与EB交于点G,现将长方形折叠,使頂点C落在HG上的D点处,折痕为EF,点F为折痕与y轴的交点.
,过点H且平行于y轴的HG与EB交于点G,现将长方形折叠,使頂点C落在HG上的D点处,折痕为EF,点F为折痕与y轴的交点.
(1)求点D的坐标;
(2)求折痕EF所在直线的函数表达式;
(3)若点P在直线AB上,当△PFD为等腰三角形时,试问满足条件的点P有几个?请求出点P的坐标,并写出解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D是矩形的四个顶点,AB=16cm,BC=6cm,动点P从点A出发,以3cm/s的速度向点B运动,直到点B为止;动点Q同时从点C出发,以2cm/s的速度向点D运动,当时间为_______时,点P和点Q之间的距离是10cm

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,其顶点
两点,其顶点![]() 在折线
在折线![]() 上移动,若点
上移动,若点![]() 、
、![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() ,点
,点![]() 的横坐标的最小值为
的横坐标的最小值为![]() ,则点
,则点![]() 的横坐标的最大值为( )
的横坐标的最大值为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com