
根据要求,解答下列问题:
(1)已知直线l1的函数表达式 为
为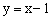 ,直接
,直接 写出:①过原点且与l1垂直的直线l2的函数表达式;②过点(1,0)且与l1垂直的直线l2的函数表达式;
写出:①过原点且与l1垂直的直线l2的函数表达式;②过点(1,0)且与l1垂直的直线l2的函数表达式;
(2)如图,过点(1,0)的直线l4向上的方向与x轴的正方 向所成的角为600,①求直线l4的函数表达式;②把直线l4绕点(1,0)按逆时针方向旋转900得到的直线l5,求直线l5的函数表达式;
向所成的角为600,①求直线l4的函数表达式;②把直线l4绕点(1,0)按逆时针方向旋转900得到的直线l5,求直线l5的函数表达式;
(3)分别观察(1)(2)中的 两个函数表达式,请猜想:当两直线垂直时,它们的函数表达式中自变量的系数之间
两个函数表达式,请猜想:当两直线垂直时,它们的函数表达式中自变量的系数之间 有何关系?请根据猜想结论直接写出过点(1,0)且与直线
有何关系?请根据猜想结论直接写出过点(1,0)且与直线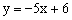 垂直的直线l6的函数表达式。
垂直的直线l6的函数表达式。

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC 于H,折痕为EF,联结BP、BH.
于H,折痕为EF,联结BP、BH.
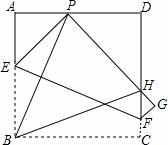
(1)求证:∠APB=∠BPH;
(2)求证:AP+ HC=PH;
HC=PH;
(3)当AP=1时,求PH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:对于实数a,符号[a]表示不大于a的最大整数.
 例如:[5.7]=5,[5]=5,[-π]=-4.
例如:[5.7]=5,[5]=5,[-π]=-4.
(1)如果[a]=-2,那么a的取值范围是 ___________.
(2)如果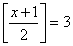
 ,满足条件的所有正整数
,满足条件的所有正整数 x有___________
x有___________ _.
_.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC= 8cm.点D、E、F分别是
8cm.点D、E、F分别是 边AB,BC,AC的中点,连接DE,DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止;
边AB,BC,AC的中点,连接DE,DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止; 点Q沿BC的方向运动,当点P停止运动时
点Q沿BC的方向运动,当点P停止运动时 ,点Q
,点Q 也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQ
也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQ N与矩形FDEC重叠部分的面积为y(cm2)(这里规定线段是面积为0有几何图形),点P运动的时间为x(s)
N与矩形FDEC重叠部分的面积为y(cm2)(这里规定线段是面积为0有几何图形),点P运动的时间为x(s)
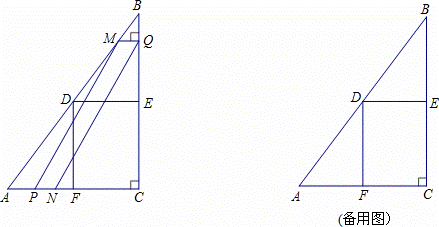
(1)当点P运动到点F时,CQ= cm;
(2)在点P从点F运动到点D的过程中,某一时刻,点P落在MQ上,求此时BQ的长度;
(3)当点P在线段FD上运动时,求y与x之间的函数关 系式.
系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
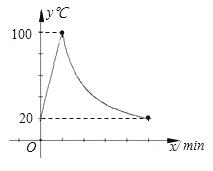
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温 开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至20℃,饮水机关机。饮水机关机后即刻自动开机,重复上述
开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至20℃,饮水机关机。饮水机关机后即刻自动开机,重复上述 自动程序。若在水温为20℃时,接通电源后,水温y(℃)和时间(min)
自动程序。若在水温为20℃时,接通电源后,水温y(℃)和时间(min) 的关系如图,为了在下午第一节下课时(14:30)能喝到健康卫生和
的关系如图,为了在下午第一节下课时(14:30)能喝到健康卫生和 水温适中的水(水沸腾后水温在20℃和50℃之间,含20℃和50℃),则接通电源的时间最晚是当天下午的
水温适中的水(水沸腾后水温在20℃和50℃之间,含20℃和50℃),则接通电源的时间最晚是当天下午的  之间。
之间。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线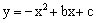 的顶点为D(﹣1,4),与
的顶点为D(﹣1,4),与 轴交于点C(0,3),与
轴交于点C(0,3),与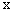 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。
(1)求抛物线的解析式;
(2)连接AC,CD,AD,试证明△ACD为直角三角形;
(3)若点E在抛物线上,EF⊥x轴于点F,以A、E、F为顶点的三角形与△ACD相似,试求出所有满足条件的点E的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com