
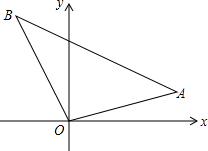
 如图,Rt△ABO在平面直角坐标系内,A(a,3),B(-4,b).若OA=6,AB=10.回答问题:
如图,Rt△ABO在平面直角坐标系内,A(a,3),B(-4,b).若OA=6,AB=10.回答问题:分析 (1)根据勾股定理求得即可;
(2)根据勾股定理求得OB,进而关键勾股定理求得即可;
(2)直接根据三角形面积计算即可或根据S△AOB=S梯形BMNA-S△BOM-S△AON即可求得.
解答 解:(1)由题意得,a2+32=62,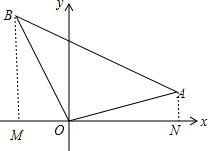
∵a>0,
∴a=3$\sqrt{3}$;
(2)∵Rt△ABO在平面直角坐标系内,OA=6,AB=10.
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=8,
由题意得,(-4)2+b2=82,
∵b>0,
∴b=4$\sqrt{3}$;
(3)方法一:S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×6×8=24;
方法二:作BM⊥x轴,AN⊥y轴,
S△AOB=S梯形BMNA-S△BOM-S△AON=$\frac{1}{2}$×(4$\sqrt{3}$+3)-$\frac{1}{2}$×4×4$\sqrt{3}$-$\frac{1}{2}$×3$\sqrt{3}$×3=24.
点评 本题考查了坐标与图形的性质,三角形的面积以及勾股定理的应用,勾股定理的应用是解题的关键.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:选择题
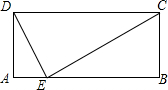 矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )| A. | 有一个点 | B. | 有两个点 | C. | 不存在 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视,它正在播广告 | |
| B. | 掷两枚质地均匀的骰子,点数之和一定大于6 | |
| C. | 某射击运动员射击一次,命中靶心 | |
| D. | 早晨的太阳从东方升起 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
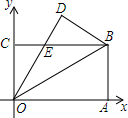 如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )
如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,$\sqrt{3}$) | C. | (2,$\sqrt{3}$) | D. | ($\frac{3}{2}$,$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com