
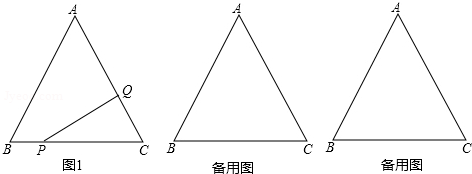
分析 分两种情况讨论:①当0<t≤4时,作QD⊥BC于D,则BP=t,PC=8-t,CQ=2t,在Rt△CDQ中,利用含30度的直角三角形三边的关系得到DC的长,利用三角形面积公式即可得出结论;
②当4≤t≤8,作QD⊥BC于D,则BP=t,PC=8-t,AQ+AC=2t,BQ=16-2t,在Rt△BDQ中,利用含30度的直角三角形三边的关系得到BD=BQ,QD=BD,然后根据三角形面积公式得到S的表达式.
解答 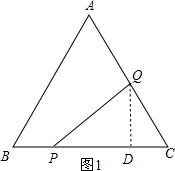 解:①当点Q在CA上运动时,即0<t≤4时,作QD⊥BC于D,如图1,
解:①当点Q在CA上运动时,即0<t≤4时,作QD⊥BC于D,如图1,
BP=t,PC=8-t,CQ=2t,
∵△ABC为等边三角形,
∴∠C=60°,
在Rt△CDQ中,DC=$\frac{1}{2}$CQ=t,
∴QD=$\sqrt{3}$CD=$\sqrt{3}$t,
∴S=$\frac{1}{2}$QD•PC=$\frac{1}{2}$•$\sqrt{3}$t•(8-t)=-$\frac{\sqrt{3}}{2}$t2+4$\sqrt{3}$t,
即△PCQ的面积S与t的函数关系式为S=-$\frac{\sqrt{3}}{2}$t2+4$\sqrt{3}$t(0<t≤4);
②当点Q在AB上运动时,即4≤t≤8,作QD⊥BC于D,如图2,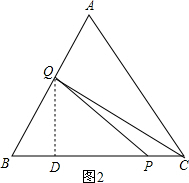 BP=t,PC=8-t,AQ+AC=2t,则BQ=16-2t,
BP=t,PC=8-t,AQ+AC=2t,则BQ=16-2t,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BDQ中,BD=$\frac{1}{2}$BQ=$\frac{1}{2}$(16-2t)=8-t,
∴QD=$\sqrt{3}$BD=$\sqrt{3}$(8-t),
∴S=$\frac{1}{2}$QD•PC=$\frac{1}{2}$•$\sqrt{3}$(8-t)•(8-t)=$\frac{\sqrt{3}}{2}$t2-8$\sqrt{3}$t+32$\sqrt{3}$,
即△PCQ的面积S与t的函数关系式为S=$\frac{\sqrt{3}}{2}$t2-8$\sqrt{3}$t+32$\sqrt{3}$(4≤t≤8).
点评 本题考查的是动点问题的函数图象,在解答此题时要注意分两种情况进行讨论,同时要作出辅助线,构造出直角三角形求解.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:选择题
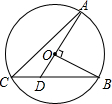 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )| A. | 65° | B. | 45° | C. | 25° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
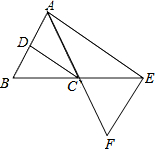 如图,已知△ABC中,CD为∠ACB的平分线,AE∥CD交BC的延长线于E,EF⊥AE交AC的延长线于F.
如图,已知△ABC中,CD为∠ACB的平分线,AE∥CD交BC的延长线于E,EF⊥AE交AC的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
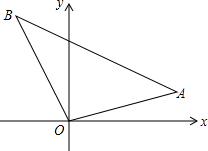 如图,Rt△ABO在平面直角坐标系内,A(a,3),B(-4,b).若OA=6,AB=10.回答问题:
如图,Rt△ABO在平面直角坐标系内,A(a,3),B(-4,b).若OA=6,AB=10.回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
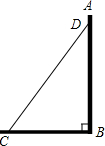 如图,将一长为6米的梯子CD斜靠在墙面上,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与地面的距离BD的长为( )米.
如图,将一长为6米的梯子CD斜靠在墙面上,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与地面的距离BD的长为( )米.| A. | 6cos55° | B. | $\frac{6}{sin55°}$ | C. | 6sin55° | D. | $\frac{6}{cos55°}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com