
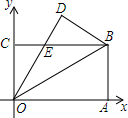
 如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )
如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,$\sqrt{3}$) | C. | (2,$\sqrt{3}$) | D. | ($\frac{3}{2}$,$\sqrt{3}$) |
分析 由折叠的性质得出∠BOD=∠AOB=30°,求出∠COE=30°,由矩形的性质得出OC=AB=$\sqrt{3}$,由三角函数求出CE,即可得出点E的坐标.
解答 解:由折叠的性质得:∠BOD=∠AOB=30°,
∴∠COE=90°-30°-30°=30°,
∵四边形OABC是矩形,
∴OC=AB,∠OCE=90°,
∵点B的坐标为(3,$\sqrt{3}$),
∴OC=AB=$\sqrt{3}$,
∴CE=OC•tan∠COE=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1,
∴点E的坐标为(1,$\sqrt{3}$);
故选:A.
点评 本题考查了翻折变换的性质、矩形的性质、三角函数;熟练掌握翻折变换和矩形的性质,由三角函数求出CE是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 该调查的方式是普查 | |
| B. | 这800名学生对“世界读书日”的知晓情况的全体是总数 | |
| C. | 每名学生对“世界读书日”的知晓情况是个体 | |
| D. | 样本容量是100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
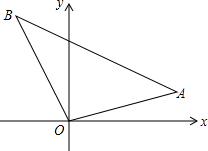 如图,Rt△ABO在平面直角坐标系内,A(a,3),B(-4,b).若OA=6,AB=10.回答问题:
如图,Rt△ABO在平面直角坐标系内,A(a,3),B(-4,b).若OA=6,AB=10.回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
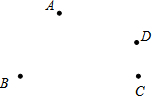 如图,已知A、B、C、D四点,根据下列要求画图:
如图,已知A、B、C、D四点,根据下列要求画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
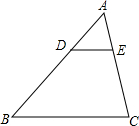 如图,在△ABC中,DE∥BC交AB于点D,交AC于点E,若DE=3,BC=9,则$\frac{AE}{AC}$=$\frac{1}{3}$.
如图,在△ABC中,DE∥BC交AB于点D,交AC于点E,若DE=3,BC=9,则$\frac{AE}{AC}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com