
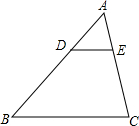
 如图,在△ABC中,DE∥BC交AB于点D,交AC于点E,若DE=3,BC=9,则$\frac{AE}{AC}$=$\frac{1}{3}$.
如图,在△ABC中,DE∥BC交AB于点D,交AC于点E,若DE=3,BC=9,则$\frac{AE}{AC}$=$\frac{1}{3}$.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 2m、2n-3 | B. | 2m-3、n | C. | m-3、2n | D. | 2m-3、4n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视,它正在播广告 | |
| B. | 掷两枚质地均匀的骰子,点数之和一定大于6 | |
| C. | 某射击运动员射击一次,命中靶心 | |
| D. | 早晨的太阳从东方升起 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
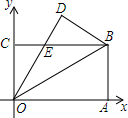 如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )
如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,$\sqrt{3}$) | C. | (2,$\sqrt{3}$) | D. | ($\frac{3}{2}$,$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x-1)2 | B. | y=2(x+1)2 | C. | y=2x2-1 | D. | y=2x2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )
如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 70.78×108元 | B. | 7.078×108元 | C. | 7.078×109元 | D. | 7.078×1010元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
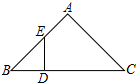 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )| A. | DE=DB | B. | DE=AE | C. | AE=BE | D. | AE=BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com