
���� ��1�������̵ĸ�Ϊy����y=-x����x=-y�����������֪���̣�Ȼ����ת��Ϊһ����ʽ���ɣ�
��2�������̵ĸ�Ϊy����y=$\frac{1}{x}$�����������֪���̣�Ȼ����ת��Ϊһ����ʽ���ɣ�
��� �⣺��1�������̵ĸ�Ϊy����y=-x����x=-y��
��x=-y������֪����x2+x-2=0��
�� ��-y��2+��-y��-2=0��
����ã�y2-y-2=0��
�ʴ��ǣ�y2-y-2=0��
��2�������̵ĸ�Ϊy����y=$\frac{1}{x}$������x=$\frac{1}{y}$��
��x=$\frac{1}{y}$������֪����ax2+bx+c=0��a��0����
a��$\frac{1}{y}$��2+b•$\frac{1}{y}$+c=0��
ȥ��ĸ���� a+by+cy2=0��
��c=0����ax2+bx=0�����Ƿ���ax2+bx+c=0��a��0����һ��Ϊ0�����������⣮
��c��0��
������ķ���Ϊ��cy2+by+a=0��c��0����
���� ���⿼����һԪ���η��̵Ľ⣮������Ĺؼ���Ū��������������ľ�����ⷽ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
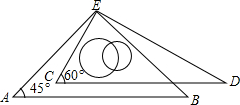 ��ͼ����һ�����dzߵ�ֱ�Ƕ����غϣ���ʹAB��CD�����AEC+��DEB�Ķ�����30�㣮
��ͼ����һ�����dzߵ�ֱ�Ƕ����غϣ���ʹAB��CD�����AEC+��DEB�Ķ�����30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
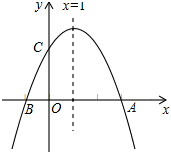 ��ͼ�����κ���y=ax2+bx+c��ͼ����x�ύA��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊx=1����B�������ǣ�-1��0�����������ĸ����ۣ���2a+b=0����4a-2b+c��0����ac��0���ܵ�y��0ʱ��x��-1��x��3��������ȷ�ĸ����ǣ�������
��ͼ�����κ���y=ax2+bx+c��ͼ����x�ύA��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊx=1����B�������ǣ�-1��0�����������ĸ����ۣ���2a+b=0����4a-2b+c��0����ac��0���ܵ�y��0ʱ��x��-1��x��3��������ȷ�ĸ����ǣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
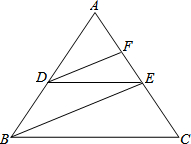 ��������������̣�
��������������̣��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com