
分析 设暗盒中有n个红球,根据暗盒中放有若干个红球和6个黑球,求出球的总个数为6+n,根据概率公式求出红球的个数,再根据在暗盒中增加2个黑球和概率公式,即可得出答案.
解答 解:设暗盒中有n个红球,
∵暗盒中有若干个红球和6个黑球,
∴球的总个数为6+n,
∵从中随机取出1个球是红球的概率是$\frac{2}{5}$,
∴$\frac{n}{n+6}$=$\frac{2}{5}$,
∴n=4,
∴在暗盒中增加2个黑球,则从中随机取出1个球是红球的概率是:$\frac{4}{4+6+2}$=$\frac{1}{3}$;
故答案为:$\frac{1}{3}$.
点评 此题考查了概率公式,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
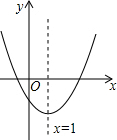 已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )
已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )| A. | a<0 | B. | c>0 | C. | 2a+b=0 | D. | 4a+2b+c>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y2>y3>y1 | D. | y3>y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
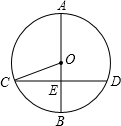 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com