
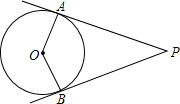
 如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )| A. | 150° | B. | 130° | C. | 155° | D. | 135° |
科目:初中数学 来源: 题型:解答题
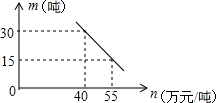 某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系,函数y与自变量x的部分对应值如表:| x(吨) | 10 | 20 | 30 |
| y(万元/吨) | 45 | 40 | 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
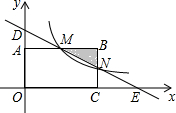 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
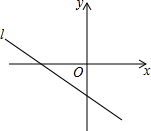 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )| A. | 1<a<2 | B. | -2<a<0 | C. | -3≤a≤-2 | D. | -10<a<-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
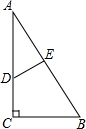 如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )| A. | ∠A和∠B互为补角 | B. | ∠B和∠ADE互为补角 | ||
| C. | ∠A和∠ADE互为余角 | D. | ∠AED和∠DEB互为余角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
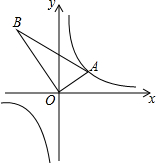 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=$\frac{1}{x}$的图象上.若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
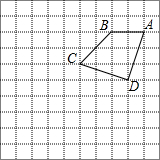 如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com