
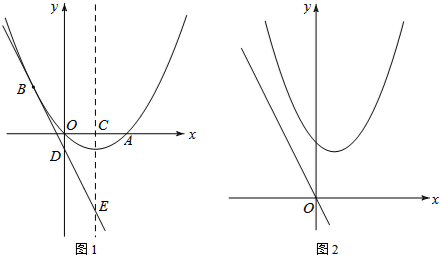
分析 (1)首先由抛物线y=ax2+bx+c经过原点O,得出c=0,那么抛物线的解析式为y=ax2+bx,再把点A(4,0)和点B(-2,3)代入y=ax2+bx,得到关于a、b的方程组,解方程组即可;
(2)先由“上加下减”的平移规律得出直线l的解析式为y=-2x-n,将点B(-2,3)代入,求出n=1,那么直线l的解析式为y=-2x-1,D(0,-1).再求出C(2,0),E(2,-5),得到点D(0,-1)是线段BE的中点.由CE=CB=5,PB=PE,得出点P是直线CD与该抛物线的交点.再用待定系数法求出CD的解析式为y=$\frac{1}{2}$x-1,将它与抛物线的解析式联立得到方程组,解方程组即可求出点P的坐标;
(3)由“上加下减”的平移规律得出新抛物线的解析式为y=$\frac{1}{4}$x2-x+6.
①设直线y=-2x向上平移t个单位能与新抛物线有交点,将y=-2x+t代入y=$\frac{1}{4}$x2-x+6,得$\frac{1}{4}$x2+x+6-t=0,由△=12-4×$\frac{1}{4}$(6-t)≥0,求出t≥5,那么t的最小值即为所求;
②先求出新抛物线与直线y=-2x+5的交点坐标为(-2,9),根据题意得出点Q坐标为(-2,9)时,到直线y=-2x的距离最短.过点Q作QR⊥直线y=-2x于点R,则RQ为所求.用待定系数法求出直线RQ的解析式为y=$\frac{1}{2}$x+10,将它与y=-2x联立得到方程组,解方程组求出R(-4,8),再根据两点间的距离公式求出RQ的长即可.
解答 解:(1)∵抛物线y=ax2+bx+c经过原点O,
∴c=0,即抛物线的解析式为y=ax2+bx,
把点A(4,0)和点B(-2,3)代入y=ax2+bx,
依题意得$\left\{\begin{array}{l}{16a+4b=0}\\{4a-2b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=-1}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{4}$x2-x;
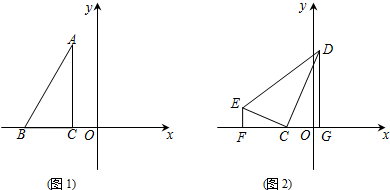
(2)如图1,将直线y=-2x沿y轴向下平移n个单位后得到直线l,则直线l的解析式为y=-2x-n,
∵直线l过点B(-2,3),
∴-2×(-2)-n=3,
解得n=1,
∴直线l的解析式为y=-2x-1,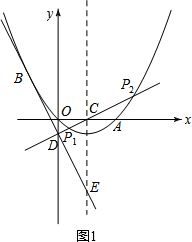 ∴D(0,-1).
∴D(0,-1).
∵抛物线y=$\frac{1}{4}$x2-x的对称轴为x=2,
∴C(2,0),E(2,-5).
∴点D(0,-1)是线段BE的中点.
又∵CE=CB=5,
∴CD垂直平分BE.
∵PB=PE,
∴点P是直线CD与该抛物线的交点.
设直线CD的解析式为y=kx+m.
将D(0,-1)、C(2,0)代入,
得$\left\{\begin{array}{l}{m=-1}\\{2k+m=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{m=-1}\end{array}\right.$,
∴CD的解析式为y=$\frac{1}{2}$x-1.
由$\left\{\begin{array}{l}y=\frac{1}{2}x-1\\ y=\frac{1}{4}{x^2}-x\end{array}\right.$,解得$\left\{\begin{array}{l}{x_1}=3+\sqrt{5}\\{y_1}=\frac{{1+\sqrt{5}}}{2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3-\sqrt{5}}\\{{y}_{2}=\frac{1-\sqrt{5}}{2}}\end{array}\right.$,
∴点P的坐标为P1(3-$\sqrt{5}$,$\frac{1-\sqrt{5}}{2}$),P2(3+$\sqrt{5}$,$\frac{1+\sqrt{5}}{2}$);
(3)将抛物线y=$\frac{1}{4}$x2-x向上平移6个单位得到新抛物线y=$\frac{1}{4}$x2-x+6.
①设直线y=-2x向上平移t个单位能与新抛物线有交点,
将y=-2x+t代入y=$\frac{1}{4}$x2-x+6,得$\frac{1}{4}$x2+x+6-t=0,
则△=12-4×$\frac{1}{4}$(6-t)≥0,
解得t≥5,
即直线y=-2x至少向上平移5个单位才能与新抛物线有交点;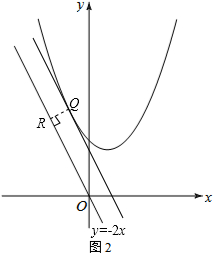 ②由$\left\{\begin{array}{l}{y=-2x+5}\\{y=\frac{1}{4}{x}^{2}-x+6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=9}\end{array}\right.$,
②由$\left\{\begin{array}{l}{y=-2x+5}\\{y=\frac{1}{4}{x}^{2}-x+6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=9}\end{array}\right.$,
即点Q坐标为(-2,9)时,到直线y=-2x的距离最短.
如图2,过点Q作QR⊥直线y=-2x于点R,则RQ为所求.
设直线RQ的解析式为y=$\frac{1}{2}$x+p,
将Q(-2,9)代入,得9=$\frac{1}{2}$×(-2)+p,
解得p=10,
则直线RQ的解析式为y=$\frac{1}{2}$x+10.
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+10}\\{y=-2x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-4}\\{y=8}\end{array}\right.$,
即R(-4,8),
又Q(-2,9),
所以RQ=$\sqrt{(-2+4)^{2}+(9-8)^{2}}$=$\sqrt{5}$.
故新抛物线上的动点Q到直线y=-2x的最短距离是$\sqrt{5}$.
点评 本题是二次函数综合题,其中涉及到的知识点有利用待定系数法求二次函数、一次函数的解析式,函数图象上点的坐标特征,抛物线与直线的平移规律,线段垂直平分线的判定,两函数交点坐标的求法,互相垂直的两条直线斜率之积为-1,二次函数与一元二次方程的关系,点到直线的距离的求法,两点间的距离公式等知识,综合性较强.利用数形结合与方程思想是解题的关键.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
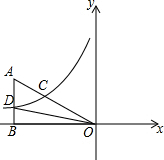 在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,连接AO.双曲线$y=\frac{k}{x}$经过斜边AO的中点C,与边AB交于点D.
在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,连接AO.双曲线$y=\frac{k}{x}$经过斜边AO的中点C,与边AB交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车主的态度 | 百分比 |
| A.没有影响 | 4% |
| B.影响不大 | p |
| C.有影响 | 52% |
| D.影响很大 | m |
| E.不关心这个问题 | 10% |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
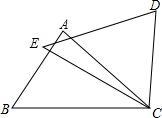 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )| A. | BC=EC,∠B=∠E | B. | BC=EC,AC=DC | C. | BC=EC,∠A=∠D | D. | ∠B=∠E,∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
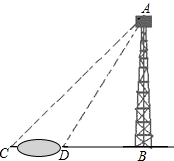 如图,AB是高为60米的铁路,分别在河边D处测得塔顶A的仰角为60°,在与BD同一直线上的河对岸C处测得塔顶A的仰角为40°.
如图,AB是高为60米的铁路,分别在河边D处测得塔顶A的仰角为60°,在与BD同一直线上的河对岸C处测得塔顶A的仰角为40°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com