
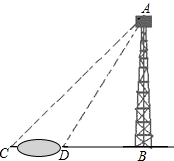
 如图,AB是高为60米的铁路,分别在河边D处测得塔顶A的仰角为60°,在与BD同一直线上的河对岸C处测得塔顶A的仰角为40°.
如图,AB是高为60米的铁路,分别在河边D处测得塔顶A的仰角为60°,在与BD同一直线上的河对岸C处测得塔顶A的仰角为40°.分析 (1)在Rt△ADB中,根据$\frac{AB}{BD}$=tan60°得到BD的长,
(2)再在Rt△ACB中,根据$\frac{60}{20\sqrt{3}+CD}$=tan40°,求出CD的长.
解答 解:在Rt△ADB中,$\frac{AB}{BD}$=tan60°,
即$\frac{60}{BD}$=$\sqrt{3}$,
解得,BD=$\frac{60}{\sqrt{3}}$=$\frac{60\sqrt{3}}{3}$=20$\sqrt{3}$米,
在Rt△ACB中,$\frac{60}{20\sqrt{3}+CD}$=tan40°,
解得CD=37.
点评 本题考查了解直角三角形的应用--仰角俯角问题,找到合适的三角形,灵活运用三角函数是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
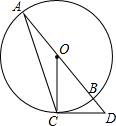 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
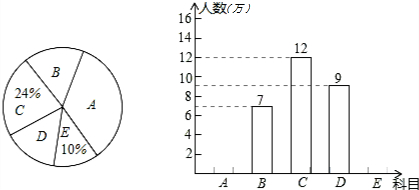 园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).
园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
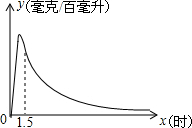 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com