
分析 (1)根据反比例函数y=$\frac{2015}{x}$的单调区间进行判断;
(2)由于二次函数y=x2-2x-k的图象开口向上,对称轴为x=1,所以二次函数y=x2-2x-k在闭区间[1,2]内,y随x的增大而增大.当x=1时,y=1,所以k=-2.当x=2时,y=2,所以k=-2.即图象过点(1,1)和(2,2)所以当1≤x≤2时,有1≤y≤2,符合闭函数的定义,所以k=-2.
(3)根据新定义运算法则,分两种情况:k>0,k<0,列出关于系数k、b的方程组,通过解该方程组即可求得系数k、b的值,即可解答.
解答 解:(1)反比例函数y=$\frac{2015}{x}$是闭区间[1,2015]上的“闭函数”.理由如下:
反比例函数y=$\frac{2015}{x}$在第一象限,y随x的增大而减小,
当x=1时,y=2015;
当x=2015时,y=1,
即图象过点(1,2015)和(2015,1)
∴当1≤x≤2015时,有1≤y≤2015,符合闭函数的定义,
∴反比例函数y=$\frac{2015}{x}$是闭区间[1,2015]上的“闭函数”;
(2)由于二次函数y=x2-2x-k的图象开口向上,
对称轴为x=1,
∴二次函数y=x2-2x-k在闭区间[1,2]内,y随x的增大而增大.
当x=1时,y=1,
∴k=-2.
当x=2时,y=2,
∴k=-2.
即图象过点(1,1)和(2,2)
∴当1≤x≤2时,有1≤y≤2,符合闭函数的定义,
∴k=-2.
(3)因为一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,
根据一次函数的图象与性质,有:
(Ⅰ)当k>0时,即图象过点(m,m)和(n,n)$\left\{\begin{array}{l}mk+b=m\\ nk+b=n\end{array}\right.$,
解得$\left\{{\begin{array}{l}{k=1}\\{b=0}\end{array}}\right.$.
∴y=x,
(Ⅱ)当k<0时,即图象过点(m,n)和(n,m),
可得:$\left\{\begin{array}{l}mk+b=n\\ nk+b=m\end{array}\right.$,解得$\left\{{\begin{array}{l}{k=-{1_{,}}}\\{b=m+n}\end{array}}\right.$
∴y=-x+m+n,
∴一次函数的解析式为y=x或y=-x+m+n.
点评 本题考查的是反比例函数的性质,解题的关键是弄清楚“闭函数”的定义.解题时,也要注意“分类讨论”数学思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
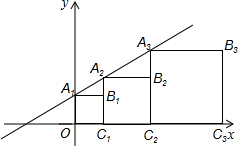 在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是(15,8),点Bn的坐标是(2n-1,2n-1).
在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是(15,8),点Bn的坐标是(2n-1,2n-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
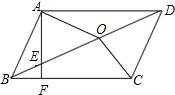 如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )
如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
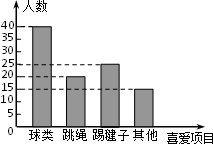 某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )
某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AC与⊙O相切于点D,连接并延长AO交⊙O于点B,过点B作BC⊥AC交于点C,交⊙O于点E,过点D作DF⊥AB垂足为F.
如图,AC与⊙O相切于点D,连接并延长AO交⊙O于点B,过点B作BC⊥AC交于点C,交⊙O于点E,过点D作DF⊥AB垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com