
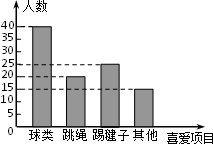
 某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )
某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{20}$ |
科目:初中数学 来源: 题型:解答题
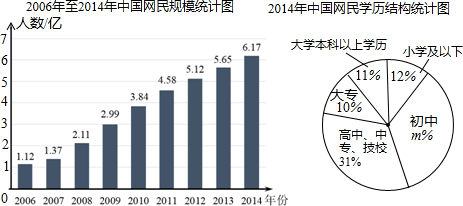
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
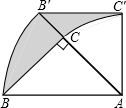 如图,在△ABC中,∠ACB=90°,BC=AC=2,以点A为旋转中心,把△ABC按顺时针方向旋转45°后得到△AB′C′,BC边在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{1}{2}$π(结果保留π).
如图,在△ABC中,∠ACB=90°,BC=AC=2,以点A为旋转中心,把△ABC按顺时针方向旋转45°后得到△AB′C′,BC边在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{1}{2}$π(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com