
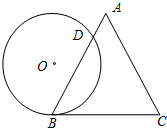
 如图,一个边长为8cm的等边△ABC的高与⊙O的直径相等,⊙O与BC相切于点B,⊙O与AB相交于点D,求BD的长.
如图,一个边长为8cm的等边△ABC的高与⊙O的直径相等,⊙O与BC相切于点B,⊙O与AB相交于点D,求BD的长. 分析 过点A作AF⊥BC,垂足为F,连接OB,根据等边三角形的性质,等边三角形的高等于底边的$\frac{\sqrt{3}}{2}$倍.已知边长为8cm的等边三角形ABC与⊙O等高,说明⊙O的半径为,即O=2$\sqrt{3}$又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FB的长,利用垂径定理即可得出BD的长.
解答 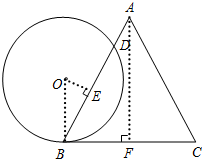 解:过点A作AF⊥BC,垂足为F,连接OB,
解:过点A作AF⊥BC,垂足为F,连接OB,
∵△ABC是等边三角形,
∴∠ABC=60°,
在Rt△ABF中,AB=8,∠ABC=60°,
∴AF=AB•sin60°=8×$\frac{{\sqrt{3}}}{2}$=4$\sqrt{3}$,
又∵△ABC的高与⊙O的直径相等,
∴⊙O的直径为4$\sqrt{3}$,
∴OB=2$\sqrt{3}$,
又∵⊙O与BC相切于点B,
∴∠OBC=90°,
∴∠OBA=30°,
过点O作OE⊥BD,垂足为E,
∴BD=2BE,
在Rt△OBE中,OB=2$\sqrt{3}$,∠OBA=30°,
∴BE=OB•cos30°=2$\sqrt{3}$×$\frac{{\sqrt{3}}}{2}$=3,
∴BD=6(cm).
点评 本题主要考查了切线的性质和等边三角形的性质和解直角三角形的有关知识.题目不是太难,属于基础性题目.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
 已知抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,与y轴交于点C.
已知抛物线y=ax2+bx-8(a≠0)经过A(-2,0),B(4,0)两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
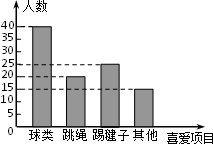 某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )
某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
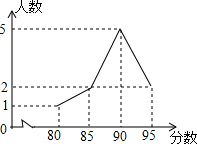 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )| A. | 众数是90分 | B. | 中位数是90分 | C. | 平均数是90分 | D. | 极差是15分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AC与⊙O相切于点D,连接并延长AO交⊙O于点B,过点B作BC⊥AC交于点C,交⊙O于点E,过点D作DF⊥AB垂足为F.
如图,AC与⊙O相切于点D,连接并延长AO交⊙O于点B,过点B作BC⊥AC交于点C,交⊙O于点E,过点D作DF⊥AB垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com