
ЁОЬтФПЁПЃЈ9ЗжЃЉФГаЃдкЛљЕиВЮМгЩчЛсЪЕМљЛАЖЏжаЃЌДјЖгРЯЪІПМЮЪбЇЩњЃКЛљЕиМЦЛЎаТНЈвЛИіОиаЮЕФЩњЮядАЕиЃЌвЛБпППОЩЧНЃЈЧНзуЙЛГЄЃЉЃЌСэЭтШ§БпгУзмГЄ69УзЕФВЛатИжеЄРИЮЇГЩЃЌгыЧНЦНааЕФвЛБпСєвЛИіПэЮЊ3УзЕФГіШыПкЃЌШчЭМЫљЪОЃЌШчКЮЩшМЦВХФмЪЙдАЕиЕФЖјЛ§зюДѓЃПЯТУцЪЧСНЮЛбЇЩњељвщЕФЧщОГЃК
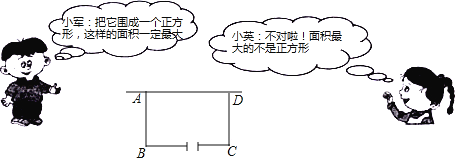
ЧыИљОнЩЯУцЕФаХЯЂЃЌНтОіЮЪЬтЃК
ЃЈ1ЃЉЩшAB=xУзЃЈxЃО0ЃЉЃЌЪдгУКЌxЕФДњЪ§ЪНБэЪОBCЕФГЄЃЛ
ЃЈ2ЃЉЧыФуХаЖЯЫЕФЫЕЗЈе§ШЗЃЌЮЊЪВУДЃП
ЁОД№АИЁПЃЈ1ЃЉBC=72Љ2xЃЈ2ЃЉаЁгЂЫЕЗЈе§ШЗ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЁЂBCЕФГЄЖШ=ЮЇРИЕФГЄЖШ-ABКЭCDЕФГЄЖШ+УХЕФПэЖШЃЛЃЈ2ЃЉЁЂЪзЯШЧѓГіSКЭxЕФЖўДЮКЏЪ§ЙиЯЕЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪЧѓГіSШЁзюДѓжЕЪБxЕФжЕЃЌДгЖјЕУГіОиаЮВЛЪЧе§ЗНаЮ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЁЂЩшABЃНxУзЃЌПЩЕУBCЃН54Љ2xЃЋ2ЃН56Љ2xЃЛ
ЃЈ2ЃЉЁЂаЁОъЕФЫЕЗЈе§ШЗЃЛ
ОиаЮУцЛ§SЃНxЃЈ56Љ2xЃЉЃНЉ2ЃЈxЉ14ЃЉ2ЃЋ392ЃЌ
Ёп56Љ2xЃО0ЃЌ
ЁрxЃМ28ЃЌ
Ёр0ЃМxЃМ28ЃЌ
ЁрЕБxЃН14ЪБЃЌSШЁзюДѓжЕЃЌ
ДЫЪБx![]() 56Љ2xЃЌ
56Љ2xЃЌ
ЁрУцЛ§зюДѓЕФВЛЪЧе§ЗНаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкСтаЮABCDжаЃЌЁЯABCЃН60Ёу
(1)ШчЭМ1ЃЌPЪЧБпBDбгГЄЯпЩЯвЛЕуЃЌвдAPЮЊБпЯђгвзїЕШБпЁїAPEЃЌСЌНгBEЁЂCE.
ЂйЧѓжЄЃКCEЁЭADЃЛ
ЂкШєABЃН![]() ЃЌBEЃН
ЃЌBEЃН![]() ЃЌЧѓAEЕФГЄЃЛ
ЃЌЧѓAEЕФГЄЃЛ
(2)ШчЭМ2ЃЌPЪЧБпCDЩЯвЛЕуЃЌЕуDЙигкAPЕФЖдГЦЕуЮЊEЃЌСЌНгBEВЂбгГЄНЛAPЕФбгГЄЯпгкЕуFЃЌСЌНгDEЁЂDF.ШєBEЃН11ЃЌDEЃН5ЃЌЧѓЁїADFЕФУцЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАыОЖЮЊ1ЕФ![]() гы
гы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЌдВаФ
СНЕуЃЌдВаФ![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЖўДЮКЏЪ§
ЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓОЙ§
ЕФЭМЯѓОЙ§![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЖЅЕуЮЊ
ЃЌЖЅЕуЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() .
.
(1)ЧѓЖўДЮКЏЪ§ЕФНтЮіЪН.
(2)ОЙ§зјБъдЕу![]() ЕФжБЯп
ЕФжБЯп![]() гы
гы![]() ЯрЧаЃЌЧѓжБЯп
ЯрЧаЃЌЧѓжБЯп![]() ЕФНтЮіЪН.
ЕФНтЮіЪН.
(3)ЪдЮЪдк![]() жсЩЯЪЧЗёДцдкЕу
жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжмГЄзюаЁЃПШєДцдкЃЌЧыЧѓГіЕу
ЕФжмГЄзюаЁЃПШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
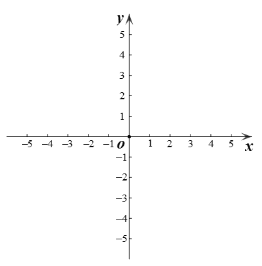
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯп![]() ЕФЖдГЦжсгыxжсНЛгкЕуA.
ЕФЖдГЦжсгыxжсНЛгкЕуA.
ЃЈ1ЃЉAЕФзјБъЮЊ ЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉШєХзЮяЯпгыxжсНЛгкPЃЌQСНЕуЃЌЧвPQ=2ЃЌЧѓХзЮяЯпЕФНтЮіЪН.
ЃЈ3ЃЉЕуBЕФзјБъЮЊ![]() ЃЌШєИУХзЮяЯпгыЯпЖЮABЧЁгавЛИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌжБНгаДГіaЕФШЁжЕЗЖЮЇ.
ЃЌШєИУХзЮяЯпгыЯпЖЮABЧЁгавЛИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌжБНгаДГіaЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
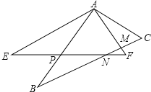
ЃЈ1ЃЉЧыЫЕУї![]() ЕФРэгЩЃЛ
ЕФРэгЩЃЛ
ЃЈ2ЃЉ![]() ПЩвдОЙ§ЭМаЮЕФБфЛЛЕУЕН
ПЩвдОЙ§ЭМаЮЕФБфЛЛЕУЕН![]() ЃЌЧыФуУшЪіетИіБфЛЛЃЛ
ЃЌЧыФуУшЪіетИіБфЛЛЃЛ
ЃЈ3ЃЉЧѓ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
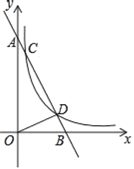
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпABгыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуAЃЌжБЯпABгыЗДБШР§КЏЪ§yЃН![]() ЃЈmЃО0ЃЉдкЕквЛЯѓЯоЕФЭМЯѓНЛгкЕуCЁЂЕуDЃЌЦфжаЕуCЕФзјБъЮЊЃЈ1ЃЌ8ЃЉЃЌЕуDЕФзјБъЮЊЃЈ4ЃЌnЃЉЃЎ
ЃЈmЃО0ЃЉдкЕквЛЯѓЯоЕФЭМЯѓНЛгкЕуCЁЂЕуDЃЌЦфжаЕуCЕФзјБъЮЊЃЈ1ЃЌ8ЃЉЃЌЕуDЕФзјБъЮЊЃЈ4ЃЌnЃЉЃЎ
ЃЈ1ЃЉЗжБ№ЧѓmЁЂnЕФжЕЃЛ
ЃЈ2ЃЉСЌНгODЃЌЧѓЁїADOЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЈЉ5ЃЌ0ЃЉЃЌвдOAЮЊжБОЖдкЕкЖўЯѓЯоФкзїАыдВCЃЌЕуBЪЧИУАыдВжмЩЯвЛЖЏЕуЃЌСЌНгOBЁЂABЃЌзїЕуAЙигкЕуBЕФЖдГЦЕуDЃЌЙ§ЕуDзїxжсДЙЯпЃЌЗжБ№НЛжБЯпOBЁЂxжсгкЕуEЁЂFЃЌЕуFЮЊДЙзуЃЌЕБDF=4ЪБЃЌЯпЖЮEF=_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
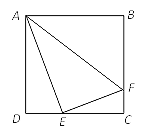
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮABCDЕФБпГЄЮЊ8ЃЌЕуEЪЧDCЩЯЕФвЛЖЏЕуЃЌЙ§ЕузїEFЁЭAEЃЌНЛBCгкЕуFЃЌСЌНсAF.
ЃЈ1ЃЉжЄУїЃКЁїADEЁзЁїECFЃЛ
ЃЈ2ЃЉШєЁїADEЕФжмГЄгыЁїECFЕФжмГЄжЎБШЮЊ4ЃК3ЃЌЧѓBFЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
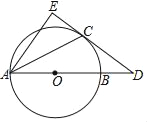
ЁОЬтФПЁПШчЭМЃЌЕуDдкЁбOЕФжБОЖABЕФбгГЄЯпЩЯЃЌCDЧаЁбOгкЕуCЃЌAEЁЭCDгкЕуE
ЃЈ1ЃЉЧѓжЄЃКACЦНЗжЁЯDAEЃЛ
ЃЈ2ЃЉШєABЃН6ЃЌBDЃН2ЃЌЧѓCEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com