
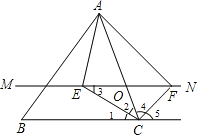
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.

【答案】(1)见解析;(2)运动到AC的中点时;(3)运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时
【解析】试题解析:(1)根据平行线性质和角平分线性质及,由平行线所夹的内错角相等易证;
(2)当点O运动到AC的中点时,四边形AECF是矩形,根据矩形的判定方法,即一个角是直角的平行四边形是矩形可证.
(3))由OE=OF,OA=OC可判断四边形AECF为平行四边形,再证明∠ECF=90°,则可判断四边形AECF为矩形,根据正方形的判定方法,当∠2=45°时,四边形AECF为正方形,于是可得∠ACB=90°.
试题解析:(1)证明:∵CE平分∠ACB,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.
理由如下:
∵EO=FO,点O是AC的中点.
∴四边形AECF是平行四边形,
∵CF平分∠BCA的外角,
∴∠4=∠5,
又∵∠1=∠2,
∴∠2+∠4=![]() ×180°=90°.
×180°=90°.
即∠ECF=90度,
∴四边形AECF是矩形.
(3)∵OE=OF,OA=OC,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,CF平分∠ACB的外角,
∴∠ECF=90°,
∴四边形AECF为矩形,
当∠2=45°时,四边形AECF为正方形,
此时∠ACB=90°,
即当点O是AC的中点,△ABC中∠ACB=90°时,四边形AECF是正方形.


科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

⑴ 作出△![]() 绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
(2)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标 .(写出一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
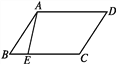
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;当A、B两点都不在原点时,如图2,点A、B都在原点的右边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;如图3,点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;如图4,点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=a+(-b)=∣a-b∣;

回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 .
(2)数轴上表示x和-1的两点A和B之间的距离是 ,如果∣AB∣=2,那么x为 ;
(3)当代数式∣x+1∣+∣x-2∣取最小值时,相应的x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上,不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②,其中AN表示平板电脑,M为AN上的定点,AN=CB=20cm,AM=8cm,MB=MN,我们把∠ANB叫做倾斜角,根据以上数据,判断倾斜角能小于30°吗?请说明理由.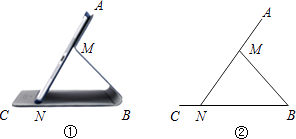
查看答案和解析>>
科目:初中数学 来源: 题型:
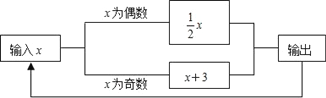
【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=
,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE= ![]() ;④S△DEF=4
;④S△DEF=4 ![]() ,其中正确的是( )
,其中正确的是( ) 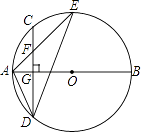
A.①②③
B.②③④
C.①②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“好书伴我成长”的读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数.统计数据如下表所示:

(1)求这50个样本数据的平均救,众数和中位数.
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com