
分析 (1)直接根据平均速度公式求得小球的平均速度;
(2)利用等量关系:速度×时间=路程,时间为ts,根据题意列出代数式:$\frac{5+(5-2t)}{2}$;
(3)利用(2)中的代数式乘时间得出路程列出方程解答即可.
解答 解:(1)$\frac{6+0}{3}$=2(m/s).
故小球的滚动速度平均每秒减少2m/s;
(2)球滚动到5m时约用了ts,
则这段时间内小球的平均速度为:$\frac{5+(5-2t)}{2}$m/s;
(3)依题意,得:t•$\frac{5+(5-2t)}{2}$=5,
整理得:t2-8t+8=0,
解得:t=4±2$\sqrt{2}$,
∵t<4,
∴t=4-2$\sqrt{2}$≈1.2.
点评 本题考查了一元二次方程的应用,重点在于求出平均每秒小球的运动减少的速度,而平均每秒小球的运动减少的速度=(初始速度-末速度)÷时间.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:选择题
| A. | 50米 | B. | 200米 | C. | 500米 | D. | 600米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{4}=\sqrt{6}$ | B. | $\root{3}{27}$=9 | C. | $\sqrt{{{(-3)}^2}}$=3 | D. | $(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})$=10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{27}$$÷\sqrt{3}$=9 | C. | $\sqrt{{4}^{2}+{3}^{2}}$=4+3=7 | D. | $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
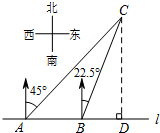 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为(2+$\sqrt{2}$)km.
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为(2+$\sqrt{2}$)km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com