
【题目】如图,四边形![]() 中的三个顶点在⊙
中的三个顶点在⊙![]() 上,
上,![]() 是优弧
是优弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).
重合).
(1)当圆心![]() 在
在![]() 内部,∠ABO+∠ADO=70°时,求∠BOD的度数;
内部,∠ABO+∠ADO=70°时,求∠BOD的度数;
(2)当点A在优弧BD上运动,四边形![]() 为平行四边形时,探究
为平行四边形时,探究![]() 与
与![]() 的数量关系.
的数量关系.

【答案】(1)140°;(2)当点A在优弧BD上运动,四边形![]() 为平行四边形时,点O在∠BAD内部时,
为平行四边形时,点O在∠BAD内部时,![]() +
+![]() =60°;点O在∠BAD外部时,|
=60°;点O在∠BAD外部时,|![]() -
-![]() |=60°.
|=60°.
【解析】
(1)连接OA,如图1,根据等腰三角形的性质得∠OAB=∠ABO,∠OAD=∠ADO,则∠OAB+∠OAD=∠ABO+∠ADO=70°,然后根据圆周角定理易得∠BOD=2∠BAD=140°;
(2)分点O在∠BAD内部和外部两种情形分类讨论:
①当点O在∠BAD内部时,
首先根据四边形OBCD为平行四边形,可得∠BOD=∠BCD,∠OBC=∠ODC;然后根据∠BAD+∠BCD=180°,∠BAD=![]() ∠BOD,求出∠BOD的度数,进而求出∠BAD的度数;最后根据平行四边形的性质,求出∠OBC、∠ODC的度数,再根据∠ABC+∠ADC=180°,求出∠OBA+∠ODA等于多少即可.
∠BOD,求出∠BOD的度数,进而求出∠BAD的度数;最后根据平行四边形的性质,求出∠OBC、∠ODC的度数,再根据∠ABC+∠ADC=180°,求出∠OBA+∠ODA等于多少即可.
②当点O在∠BAD外部时:
Ⅰ、首先根据四边形OBCD为平行四边形,可得∠BOD=∠BCD,∠OBC=∠ODC;然后根据∠BAD+∠BCD=180°,∠BAD=![]() ∠BOD,求出∠BOD的度数,进而求出∠BAD的度数;最后根据OA=OD,OA=OB,判断出∠OAD=∠ODA,∠OAB=∠OBA,进而判断出∠OBA=∠ODA+60°即可.
∠BOD,求出∠BOD的度数,进而求出∠BAD的度数;最后根据OA=OD,OA=OB,判断出∠OAD=∠ODA,∠OAB=∠OBA,进而判断出∠OBA=∠ODA+60°即可.
Ⅱ、首先根据四边形OBCD为平行四边形,可得∠BOD=∠BCD,∠OBC=∠ODC;然后根据∠BAD+∠BCD=180°,∠BAD=![]() ∠BOD,求出∠BOD的度数,进而求出∠BAD的度数;最后根据OA=OD,OA=OB,判断出∠OAD=∠ODA,∠OAB=∠OBA,进而判断出∠ODA=∠OBA+60°即可.
∠BOD,求出∠BOD的度数,进而求出∠BAD的度数;最后根据OA=OD,OA=OB,判断出∠OAD=∠ODA,∠OAB=∠OBA,进而判断出∠ODA=∠OBA+60°即可.
(1)连接OA,如图1,
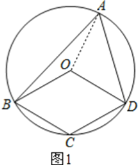
∵OA=OB,OA=OD,
∵∠OAB=∠ABO,∠OAD=∠ADO,
∴∠OAB+∠OAD=∠ABO+∠ADO=70°,即∠BAD=70°,
∴∠BOD=2∠BAD=140°;
(2)①如图2,
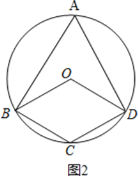 ,
,
∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,∠OBC=∠ODC,
又∵∠BAD+∠BCD=180°,∠BAD=![]() ∠BOD,
∠BOD,
∴![]() ∠BOD+∠BOD=180°,
∠BOD+∠BOD=180°,
∴∠BOD=120°,∠BAD=120°÷2=60°,
∴∠OBC=∠ODC=180°-120°=60°,
又∵∠ABC+∠ADC=180°,
∴∠OBA+∠ODA=180°-(∠OBC+∠ODC)
=180°-(60°+60°)
=180°-120°
=60°
②Ⅰ、如图3,
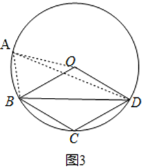 ,
,
∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,∠OBC=∠ODC,
又∵∠BAD+∠BCD=180°,∠BAD=![]() ∠BOD,
∠BOD,
∴![]() ∠BOD+∠BOD=180°,
∠BOD+∠BOD=180°,
∴∠BOD=120°,∠BAD=120°÷2=60°,
∴∠OAB=∠OAD+∠BAD=∠OAD+60°,
∵OA=OD,OA=OB,
∴∠OAD=∠ODA,∠OAB=∠OBA,
∴∠OBA-∠ODA=60°.
Ⅱ、如图4,
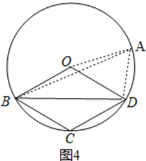 ,
,
∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,∠OBC=∠ODC,
又∵∠BAD+∠BCD=180°,∠BAD=![]() ∠BOD,
∠BOD,
∴![]() ∠BOD+∠BOD=180°,
∠BOD+∠BOD=180°,
∴∠BOD=120°,∠BAD=120°÷2=60°,
∴∠OAB=∠OAD-∠BAD=∠OAD-60°,
∵OA=OD,OA=OB,
∴∠OAD=∠ODA,∠OAB=∠OBA,
∴∠OBA=∠ODA-60°,
即∠ODA-∠OBA=60°.
所以,当点A在优弧BD上运动,四边形![]() 为平行四边形时,点O在∠BAD内部时,
为平行四边形时,点O在∠BAD内部时,![]() +
+![]() =60°;点O在∠BAD外部时,|
=60°;点O在∠BAD外部时,|![]() -
-![]() |=60°.
|=60°.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,反比例函数y=![]() (x>0,k>0图象上的两点(n,3n)、(n+1,2n).
(x>0,k>0图象上的两点(n,3n)、(n+1,2n).
(1)求n的值;
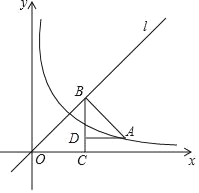
(2)如图,直线l为正比例函数y=x的图象,点A在反比例函数y=![]() (x>0,k>0)的图象上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为S1,△ABD的面积为S2,求S1﹣S2的值.
(x>0,k>0)的图象上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为S1,△ABD的面积为S2,求S1﹣S2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
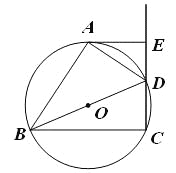
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE
(Ⅰ)求证:AE是⊙O的切线;
(Ⅱ)若∠DBC=30°,DE=1 cm,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=![]() x2-2x,直线y2=-2x+b相交于A,B两点,其中点A的横坐标为2.当x任取一值时,x对应的函数值分别为y1,y2,取m=
x2-2x,直线y2=-2x+b相交于A,B两点,其中点A的横坐标为2.当x任取一值时,x对应的函数值分别为y1,y2,取m=![]() (|y1-y2|+y1+y2).则
(|y1-y2|+y1+y2).则

A. 当x<-2时,m=y2.B. m随x的增大而减小.
C. 当m=2时,x=0.D. m≥-2.
查看答案和解析>>
科目:初中数学 来源: 题型:
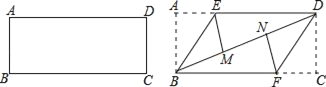
【题目】准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,BE=2,求菱形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
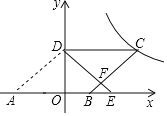
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y![]() (k≠0)图象经过点C,且S△BEF=1,则k的值为________.
(k≠0)图象经过点C,且S△BEF=1,则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是![]() ,写出表示x和y关系的表达式.
,写出表示x和y关系的表达式.
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为![]() ,求x和y的值.
,求x和y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胜利中学从全校学生中随机选取一部分学生,对他们每周上网的时间t进行调查,调查情况分为:![]() 小时;
小时;![]() 小时
小时![]() 小时;
小时;![]() 小时
小时![]() 小时;
小时;![]() 小时四种,并将统计结果制成了如下两幅不完整的统计图,请根据图中信息解答下列问题:
小时四种,并将统计结果制成了如下两幅不完整的统计图,请根据图中信息解答下列问题:
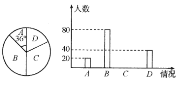
![]() 求参加调查的学生的人数;
求参加调查的学生的人数;
![]() 求扇形图中
求扇形图中![]() 组扇形的圆心角度数,并通过计算补全条形统计图;
组扇形的圆心角度数,并通过计算补全条形统计图;
![]() 在所调查的学生中,随机选取一名学生,求他每周上网时间大于
在所调查的学生中,随机选取一名学生,求他每周上网时间大于![]() 小时的概率.
小时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com