

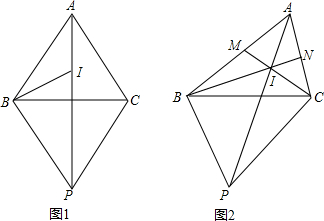
���� ��1������EC������=60��ʱ����ABC����DCE�ǵȱ������Σ�EC=DC��AC=BC�����ݵ�����������á�BCD=��ACE���ɵá�BDC�ա�ACE���𰸿�֤��
��2������D��DF��AC����BC��F����֤�á�DFB�ǵ���ֱ�������Σ�BD=DF=$\sqrt{2}$BF����֤����ADE�ס�FCD���ã�$\frac{AE}{DF}$=$\frac{AD}{CF}$����DF��AC���ã�$\frac{BD}{BF}$=$\frac{AD}{CF}$���ɵõ�$\frac{AE}{BD}$=$\frac{BD}{BF}$=$\frac{\sqrt{2}}{2}$���̶��õ��𰸣�
��3��������EC���������ĵ㹲Բ֤����ȣ�Ȼ��֤��BDC�ס�AEC���ƿ���ȷ��BD=2cos��•AE��
��� �⣺��1�����ۣ�BD=AE��
���ɣ���ͼ12������EC��AC��DE��F������=60��ʱ����ABC
��AE��BC��
���EAF=��ACB=��FDC=60�㣬�ߡ�AFE=��DFC��
���AFE�ס�DFC��
��$\frac{AF}{DF}$=$\frac{EF}{CF}$��
��$\frac{AF}{EF}$=$\frac{DF}{CF}$���ߡ�AFD=��EFC��
���AFD�ס�EFC��
���DAF=��FEC=60�㣬
���DEC�ǵȱ������Σ�
��EC=DC��AC=BC����ACB=��DCE=60�㣬
���ACB-��ACD=��DCE-��ACD��
����BCD=��ACE��
�ڡ�BDC�͡�ACE�У�
$\left\{\begin{array}{l}{EC=DC}\\{��BCD=��ACE}\\{AC=BC}\end{array}\right.$��
���BDC�ա�ACE��SAS����
��BD=AE��
��2��BD=$\sqrt{2}$AE���������£�
��ͼ2������D��DF��AC����BC��F��
��DF��AC��
���ABC=��DFB��
�ߡ�ABC=��ACB=������=45�㣬
���ABC=��ACB=��DFB=45�㣮
���DFB�ǵ���ֱ��������
��BD=DF=$\frac{\sqrt{2}}{2}$BF��
��AE��BC��
���ABC+��BAE=180�㣮
�ߡ�DFB+��DFC=180��
���BAE=��DFC��
�ߡ�ABC+��BCD=��ADC����ABC=��CDE=����
���ADE=��BCD��
���ADE�ס�FCD��
��$\frac{AE}{DF}$=$\frac{AD}{CF}$��
��DF��AC��
��$\frac{BD}{BF}$=$\frac{AD}{CF}$��
��$\frac{AE}{BD}$=$\frac{BD}{BF}$=$\frac{\sqrt{2}}{2}$��
��BD=$\sqrt{2}$AE��
��3����ȫͼ����ͼ3������EC����AE��BC����EAC=��ACB=����
���EAC=��EDC=����
��A��D��C��E�ĵ㹲Բ��
���ADE=��ACE��
�ߡ�ADE+��EDC=��ADC=��ABC+��BCD����ABC=��EDC=����
���ADE=��BCD��
���ACE=��BCD
�ߡ�ABC=��EAC=����
���BDC�ס�ACE��
��$\frac{BD}{AE}$=$\frac{BC}{AC}$��
�֡�$\frac{BC}{AC}$=2cos����
��BD=2cos��•AE��
�ʴ�ΪBD=2cos��•AE��
���� ������Ҫ�����˵ȱ������ε������Լ����������Ƶ��ж������ʵ��ۺ�Ӧ�ã��ڽ����ʱҪע�����˼���Ӧ�ã���ȷ��ͼҲ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
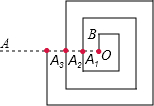 ��ͼ��һ����ͼ�������ͨ���Ŀ���OB�ij���Ϊ1��������������OA����A1��A2��A3��������O�㵽A1��Ļ�����Ϊ��1Ȧ����Ϊ7������A1�㵽A2��Ļ�����Ϊ��2Ȧ����A2�㵽A3��Ļ�����Ϊ��3Ȧ�������������ƣ����10Ȧ�ij�Ϊ79��
��ͼ��һ����ͼ�������ͨ���Ŀ���OB�ij���Ϊ1��������������OA����A1��A2��A3��������O�㵽A1��Ļ�����Ϊ��1Ȧ����Ϊ7������A1�㵽A2��Ļ�����Ϊ��2Ȧ����A2�㵽A3��Ļ�����Ϊ��3Ȧ�������������ƣ����10Ȧ�ij�Ϊ79���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
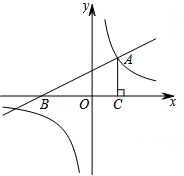 ��ͼ��һ�κ���y=$\frac{1}{2}$x+2��ͼ����x�ύ�ڵ�B���뷴��������y=$\frac{k}{x}$��ͼ���һ������ΪA��2��m����
��ͼ��һ�κ���y=$\frac{1}{2}$x+2��ͼ����x�ύ�ڵ�B���뷴��������y=$\frac{k}{x}$��ͼ���һ������ΪA��2��m�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
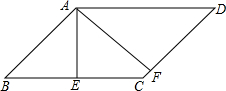 ��ͼ����ƽ���ı���ABCD�У�AE��BC��E��AF��CD��F����EAF=45�㣬��AE+AF=2$\sqrt{2}$����ƽ���ı���ABCD���ܳ��ǣ�������
��ͼ����ƽ���ı���ABCD�У�AE��BC��E��AF��CD��F����EAF=45�㣬��AE+AF=2$\sqrt{2}$����ƽ���ı���ABCD���ܳ��ǣ�������| A�� | 2 | B�� | 4$\sqrt{2}$ | C�� | 4 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 80�� | C�� | 100�� | D�� | 120�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com