
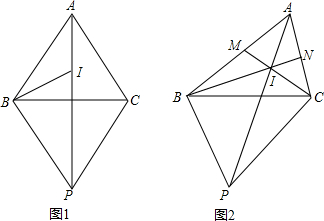
分析 (1)①由等腰三角形的性质证明∠BAC=∠BCA(设为α);由内切圆的性质求出∠ABI=90°-α,进而证明∠ABP+∠BAC=180°,即可解决问题;
②首先证明PB=BC,进而得到∠BCP=∠BPC;证明∠PBC=∠ACB=α,运用三角形的内角和定理,求出∠BCP,即可解决问题;
(2)根据△ABC为等边三角形时,P到直线BC的距离的最大求出最大值即可.
解答 解:(1)①如图,∵BA=BC,
∴∠BAC=∠BCA(设为α);
∵点I为△ABC的内心,
∴∠ABI=$\frac{180°-2α}{2}$=90°-α,
∴∠ABP=90°+90°-α=180°-α,
∴∠ABP+∠BAC=180°-α+α=180°,
∴BP∥AC.
②如图,∵BP∥AC,
∴∠CAP=∠APB,∠BCA=∠PBC,
∵AI是∠BAC的平分线,
∴∠BAP=∠CAP,
∴∠BAP=∠APB,
∴AB=PB;
∵AB=BC,
∴PB=BC,
∴∠BPC=∠BCP,
∴∠BCP=$\frac{180°-∠PBC}{2}$;
∵∠BCA=∠BAC=α,
∴∠PBC=∠BCA=∠BAC=α,
∴∠BCP=$\frac{180°-α}{2}$.
(2)当△ABC为等边三角形时,BC=BM+CN=6,
此时P到直线BC的距离的最大,
在等边三角形PBC中,BC=6,
P到直线BC的距离的最大值是3$\sqrt{3}$.
点评 该题主要考查了三角形内切圆的性质、三角形内角和定理、平行线的判定等几何知识点及其应用问题;牢固掌握三角形内切圆的性质等几何知识点是基础,灵活运用、解题是关键.


科目:初中数学 来源: 题型:解答题
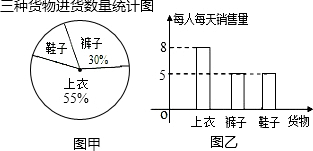
| 货物 | 上衣 (件) | 裤子 (条) | 鞋子 (双) |
| 3天的销售总量 | 72 | 30 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
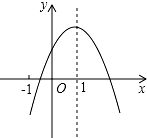 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )| A. | ①②③ | B. | ①③④ | C. | ③④⑤ | D. | ②③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com