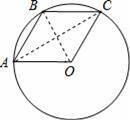
已知A，B，C是⊙O上的三个点，四边形OABC是平行四边形，那么下列结论中错误的是（ ）
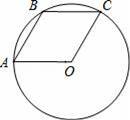
A．∠AOC=120°
B．四边形OABC一定是菱形
C．若连接AC，则AC=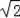
OA
D．若连接AC、BO，则AC与BO互相垂直平分
C【考点】圆周角定理；平行四边形的性质；菱形的判定．
【分析】连接OB，AC，根据已知条件得到四边形OABC一定是菱形，根据菱形的性质得到AC与BO互相垂直平分，根据等边三角形的性质得到∠BCO=60°，解直角三角形即可得到结论．
【解答】解：连接OB，AC，
∵四边形OABC是平行四边形，
∵OA=OC，
∴四边形OABC一定是菱形，
∴则AC与BO互相垂直平分，
∵OB=OC，
∴△BCO是等边三角形，
∴∠BCO=60°，
∴∠AOC=120°，
∵∠OAC=30°，
∴
AC=
OA，
∴AC=
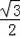
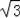
OA．
故选C．
【点评】本题考查了圆周角定理，菱形的判定和性质，解直角三角形，熟练掌握菱形的性质是解题的关键．
小学学习好帮手系列答案
小学同步三练核心密卷系列答案科目：初中数学 来源： 题型：
八年级（1）班学生在完成课题学习“体质健康测试中的数据分析”后，利用课外活动时间积极参加体育锻炼，每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练，训练后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图．
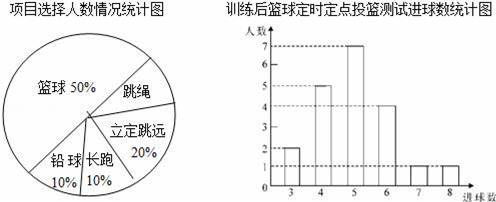
请你根据上面提供的信息回答下列问题：
（1）扇形图中跳绳部分的扇形圆心角为 度，该班共有学生 人，训练后篮球定时定点投篮平均每个人的进球数是 ．
（2）老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试，请用列表或画树形图的方法求恰好选中两名男生的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路按下面的要求填空，完成本题的解答．也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求进行解答．
要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场．根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，比赛组织者应邀多少个队参赛？
解题方案：
设比赛组织者应邀请x个队参赛，
（1）用含x的代数式表示：
那么每个队要与其他 个队各赛一场，又由于甲队对乙队的比赛和乙队对甲对的比赛是同一场比赛，所以全部的比赛一共有 场；
（2）根据题意，列出相应方程；
（3）解这个方程，得；
（4）检验： ；
（5）答： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角形的斜边上，AC与DM，DN分别交于点E、F，把△DEF绕点D旋转到一定位置，使得DE=DF，则∠BDN的度数是 ．
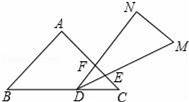
查看答案和解析>>
科目：初中数学 来源： 题型：
下列说法中正确的有（ ）
①位似图形都相似；
②两个等腰三角形一定相似；
③两个相似多边形的面积比为4：9，则周长的比为16：81；
④若一个三角形的三边分别比另一个三角形的三边长2cm，那么这两个三角形一定相似．
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
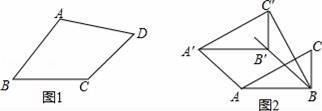
类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．
（1）如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．
（2）小红猜想：对角线互相平分的“等邻边四边形”是菱形．她的猜想正确吗？请说明理由．
（3）如图2，小红作了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′．小红要使得平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离（即线段B′B的长）？
查看答案和解析>>
科目：初中数学 来源： 题型：
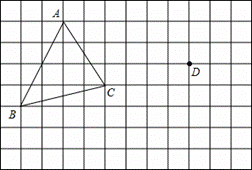
在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示．现将△ABC平移，使点A变换为点D，点E、F分别是B、C的对应点．
（1）请画出平移后的△DEF，并求△DEF的面积=
（2）若连接AD、CF，则这两条线段之间的关系是_________________；
（3）请在AB上找一点P，使得线段CP平分△ABC的面积，在图上作出线段CP.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的平方根是 ．