练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    的平方根是　　　　　　．


    　±　．

    【考点】平方根．

    【分析】直接根据正数的平方根的意义解答即可．

    【解答】解：的平方根是±．

    故答案为：±．

    【点评】本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    因式分解

    （x2+4）2﹣16x2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知A，B，C是⊙O上的三个点，四边形OABC是平行四边形，那么下列结论中错误的是（　　）

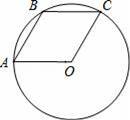
    A．∠AOC=120°

    B．四边形OABC一定是菱形

    C．若连接AC，则AC=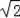OA

    D．若连接AC、BO，则AC与BO互相垂直平分

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    有五张下面分别标有数字﹣2，0，，1，3的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，则使关于x的分工方程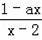+2=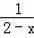有整数解的概率是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式组：并将不等式组的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，D，E分别是AB和AC上的点，满足AD=3，AE=2，EC=1，DE∥BC，则AB=（　　）

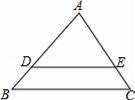
    A．6       B．4.5    C．2       D．1.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


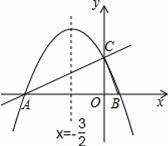
    如图，在平面直角坐标系xOy中，直线y=x+2与x轴交于点A，与y轴交于点C．抛物线y=ax2+bx+c的对称轴是x=﹣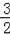且经过A、C两点，与x轴的另一交点为点B．

    （1）①直接写出点B的坐标；②求抛物线解析式．

    （2）若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P的坐标．

    （3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在五边形ABCDE中，∠A+∠B+∠E=300°，DP、CP分别平分∠EDC、∠BCD，则∠P的度数是（　　）

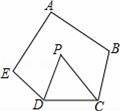
    A．60°   B．65°    C．55°   D．50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    问题背景：△AOB、△COD是两个等腰直角三角形，现将直角顶点以及两直角边都重合在一起，如图1所示，点P是CD中点，连接BP并延长到E使PE=BP，连接EC，作平行四边形ACEF，小林针对平行四边形ACEF形状进行了如下探究：

    观察操作：（1）小林先假设小等腰直角三角形的直角边非常小，这时三角形可以看作一个点，如图2所示，并提出猜想四边形ACEF是　　　　　　；

    猜想证明：（2）小林对比图1和图2的情形，完成了（1）中的猜想，请借助图1帮他证明这个猜想．

    拓展延伸：（3）如图3所示，现将等腰直角三角形COD绕点O逆时针旋转一定角度，其它条件都不改变，原来结论是否仍然成立？请说明理由．

    查看答案和解析>>

    同步练习册答案