
分析 把第1个和第2个分式的分子除1,分母除以abcd,变形后进行同分母的加法运算,再利用同样方法进行变形得到同分母,然后同分母的加法运算,最后约分即可.
解答 解:原式=$\frac{a}{\frac{1}{d}+\frac{1}{bc}+\frac{1}{bcd}+\frac{bcd}{bcd}}$+$\frac{b}{bcd+bc+b+1}$+$\frac{c}{\frac{1}{b}+\frac{1}{ab}+\frac{1}{dab}+\frac{dab}{dab}}$+$\frac{d}{bad+da+d+1}$
=$\frac{a}{\frac{bcd+bc+b+1}{bc}}$+$\frac{b}{bcd+bc+b+1}$+$\frac{c}{\frac{dab+da+d+1}{dab}}$+$\frac{d}{bad+da+d+1}$
=$\frac{abcd}{bcd+bc+b+1}$+$\frac{b}{bcd+bc+b+1}$+$\frac{abcd}{dab+da+d+1}$+$\frac{d}{dab+da+d+1}$
=$\frac{b+1}{bcd+bc+b+1}$+$\frac{1+d}{dab+da+d+1}$
=$\frac{b+1}{bcd+bc+b+1}$+$\frac{1+d}{\frac{1}{c}+\frac{1}{bc}+\frac{bcd}{bc}+\frac{bc}{bc}}$
=$\frac{b+1}{bcd+bc+b+1}$+$\frac{1+d}{\frac{bcd+bc+b+1}{bc}}$
=$\frac{b+1}{bcd+bc+b+1}$+$\frac{bc+bcd}{bcd+bc+b+1}$
=$\frac{1+b+bc+bcd}{bcd+bc+b+1}$
=1.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.解决本题的关键是运用分式的基本性质把分母化为同分母的分式.解决本题的关键是把abcd=1进行互换,把分母化为同分母.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
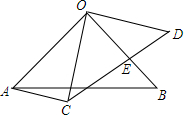 如图,已知△OAB和△0CD都是等腰直角三角形,点O是直角顶点,OA=10,OC=6$\sqrt{2}$,将△OCD绕点O旋转,使CD与OB相交于点E,当△BDE变成直角三角形时,线段AC的长为2或2$\sqrt{13}$.
如图,已知△OAB和△0CD都是等腰直角三角形,点O是直角顶点,OA=10,OC=6$\sqrt{2}$,将△OCD绕点O旋转,使CD与OB相交于点E,当△BDE变成直角三角形时,线段AC的长为2或2$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-4,-1) | B. | (1,-4) | C. | (-5,1) | D. | (-1,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知多项式m5n2-1中,含字母的项的系数为b,多项式的次数为c,常数项为a,请回答问题.
已知多项式m5n2-1中,含字母的项的系数为b,多项式的次数为c,常数项为a,请回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
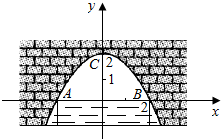 图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com