
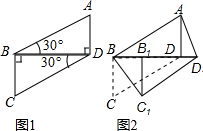
 将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).
将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).分析 (1)欲证明四边形ABC1D1是平行四边形,只需推知:AB=C1D1,AB∥C1D1即可;
(2)只要∠BC1D1=90°,四边形ABC1D1即为矩形,所以求得Rt△BB1C1的面积即可易求矩形ABC1D1的面积;
(3)当点B的移动距离为$\sqrt{3}$时,D、B1两点重合,根据对角线互相垂直平分的四边形是菱形,可判定四边形ABC1D1为菱形.
解答 (1)证明:根据平移的性质得到:△ABD≌△CDB≌△C1D1B1,
∴AB=C1D1.
又∵∠ABD=∠C1D1B=30°,
∴AB∥C1D1,
∴四边形ABC1D1是平行四边形;
(2)解:∵在移动过程中,四边形ABC1D1恒为平行四边形,
∴只要∠BC1D1=90°,四边形ABC1D1即为矩形,
此时在Rt△BB1C1中,B1C1=1,∠BB1C1=90°,∠B1BC1=60°,
∴BC1=2BB1,由勾股定理得,BC1=$\frac{2\sqrt{3}}{3}$,
由已知得:AB=2,
∴S矩形ABC1D1=$\frac{2\sqrt{3}}{3}$×2=$\frac{4\sqrt{3}}{3}$;
(3)解:当四边形ABC1D是菱形时,∠ABD1=∠C1BD1=30°,
∵B1C1=1,
∴BB1=$\frac{{B}_{1}{C}_{1}}{tan30°}$=$\frac{1}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$,
当点B的移动距离为$\sqrt{3}$时,四边形ABC1D1为菱形.
点评 此题主要考查平行四边形、矩形、菱形的判定,综合利用了直角三角形的性质,注意:有一直角的平行四边形是矩形,菱形的每一条对角线平分一组对角.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:填空题
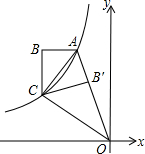 如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.
如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
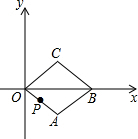 如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价格x(元/本) | … | 25 | 30 | 35 | 40 | … |
| 销售量y(本) | … | 250 | 200 | 150 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com