
| 销售价格x(元/本) | … | 25 | 30 | 35 | 40 | … |
| 销售量y(本) | … | 250 | 200 | 150 | 100 | … |
分析 (1)利用销量×每件利润=总利润,进而求出即可;
(2)利用二次函数的性质得出销售单价;
(3)分别求出两种方案的最值进而比较得出答案.
解答 解:(1)以表中x、y的对应值作为点的坐标在平面直角坐标系中描点,发现y是x的一次函数,
设y=kx+b,由题意得$\left\{\begin{array}{l}{25k+b=250}\\{40k+b=100}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-10}\\{b=500}\end{array}\right.$.
所以y=-10x+500(0<x≤50);
(2)w=(x-20)(-10x+500)
=-10x2+700x-10000=-10(x-35)2+2250.
∵-10<0,
∴函数图象开口向下,w有最大值,
当x=35时,w最大=2250,
故当单价为35元时,该文具每天的利润最大;
(3)B方案利润高.理由如下:
A方案中:20<x≤26,
故当x=26时,w有最大值,
此时wA=1440;
B方案中:$\left\{\begin{array}{l}{-10x+500≥50}\\{x-20≥18}\end{array}\right.$,
故x的取值范围为:38≤x≤45,
∴当x=38时,w有最大值,
此时wB=2160,
∵wA<wB,
∴B方案利润更高.
点评 本题考查了二次函数的应用,难度较大,最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=-$\frac{b}{2a}$时取得.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{81}$=±9 | B. | -$\sqrt{(-6)^{2}}$=6 | C. | ($\sqrt{2}$+$\sqrt{3}$)2=5 | D. | 16${\;}^{\frac{1}{2}}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
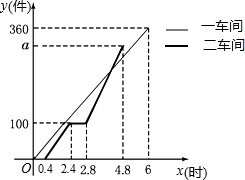 某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示:
某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
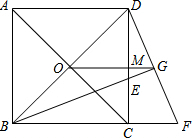 已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
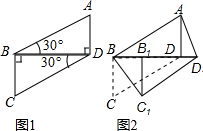 将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).
将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
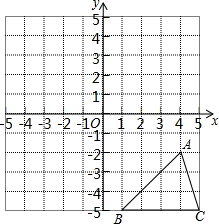 在平面直角坐标系中,按照下列要求作图:
在平面直角坐标系中,按照下列要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
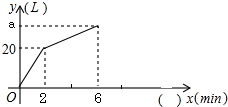 一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.
一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com