
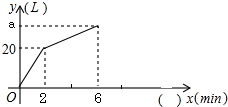
 一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.
一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.分析 (1)每分钟的进水量根据前2分钟的图象求出,根据后4分钟的水量变化即可求得a的值.
(2)用待定系数法求对应的函数关系式;
(3)根据每个出水管每分钟出水量,即可求得排完容器的水所有的时间,根据时间补全函数图象即可.
解答 解:(1)根据图象,每分钟进水20÷2=10L,
在随后的4min内容器内的水量y=4(10-7.5)=10(L),
∴a=20+10=30;
(2)设y=kx+b.
∵图象过(2,20)、(6,30),
∴$\left\{\begin{array}{l}{20=2k+b}\\{30=6k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{5}{2}}\\{b=15}\end{array}\right.$,
∴y=$\frac{5}{2}$x+15 (2≤x≤6);
(3)∵30÷(2×7.5)=2;
∴补全函数图象如图所示: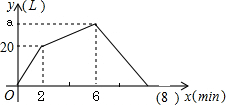
点评 此题考查了一次函数的应用问题,解题时首先正确理解题意,然后根据题意利用待定系数法确定函数的解析式,接着利用函数的性质即可解决问题.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
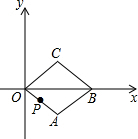 如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价格x(元/本) | … | 25 | 30 | 35 | 40 | … |
| 销售量y(本) | … | 250 | 200 | 150 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1.5 | C. | 1 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com