
分析 分类讨论:分别画出k2>0和k2<0时的图象,然后根据图象求解.
解答 解:若k2>0,如图1,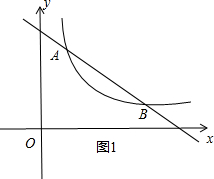
当0<x<1或x>5时,k1x+b<$\frac{{k}_{2}}{x}$,即不等式k1x<$\frac{{k}_{2}}{x}$-b的解集为0<x<1或x>5;
若k2<0,如图2,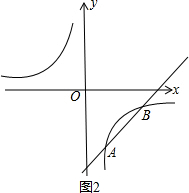
当1<x<5或x<0时,k1x+b<$\frac{{k}_{2}}{x}$,即不等式k1x<$\frac{{k}_{2}}{x}$-b的解集为1<x<5或x<0.
故答案为k2>0时,0<x<1或x>5;k2<0时,1<x<5或x<0.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.


科目:初中数学 来源: 题型:选择题
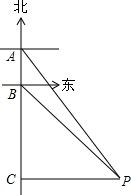 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.| A. | 10$\sqrt{3}$ | B. | 10$\sqrt{2}$-10 | C. | 10 | D. | 10$\sqrt{3}$-10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
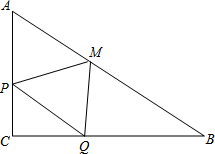 在Rt△ABC中,∠C=90°,AC=6,BC=8,直线PQ沿CA方向自C向A运动,速度为1cm/s,且总保持PQ∥AB;同时,点M从A出发沿AB方向向B运动,速度为2cm/s.设运动时间为t(0<t<4)
在Rt△ABC中,∠C=90°,AC=6,BC=8,直线PQ沿CA方向自C向A运动,速度为1cm/s,且总保持PQ∥AB;同时,点M从A出发沿AB方向向B运动,速度为2cm/s.设运动时间为t(0<t<4)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{81}$=±9 | B. | -$\sqrt{(-6)^{2}}$=6 | C. | ($\sqrt{2}$+$\sqrt{3}$)2=5 | D. | 16${\;}^{\frac{1}{2}}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
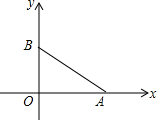 如图,线段AB的两个端点坐标分别为A($\sqrt{3}$,0)、B(0,1).
如图,线段AB的两个端点坐标分别为A($\sqrt{3}$,0)、B(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
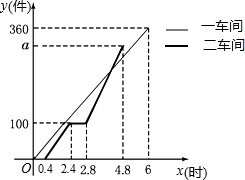 某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示:
某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
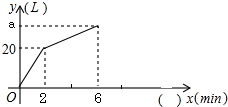 一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.
一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com