
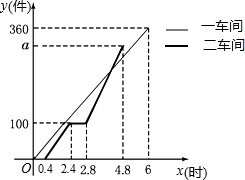
 某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示:
某工厂安排第一、二两个车间的工人加工某种商品,第一车间加工0.4小时后,第二车间开始工作,第二车间工作中有一次停产更换设备,更换设备后,第二车间的工作效率是原来的2倍,两车间各自加工商品的数量y(件)与时间x(时)的函数图象如图所示:分析 (1)设第一车间加工商品的数量y与时间x之间的函数关系式为y=kx,再利用待定系数法解出即可;
(2)根据题意列出方程解答即可;
(3)把x=2.8代入解析式y=60x解得即可;
(4)根据题意列出方程解答即可.
解答 解:(1)设第一车间加工商品的数量y与时间x之间的函数关系式为y=kx,
根据题意得:6k=360,
解得:k=60,
所以关系式为:y=60x;
(2)当x=2.8时,y=100,由第二车间更换设备后工作效率是原来的2倍,
得:$\frac{a-100}{4.8-2.8}=\frac{100}{2}×2$,
解得:a=300;
(3)把x=2.8代入解析式可得:y=60×2.8=168,
所以两车间加工出的商品总和=168+100=268(件);
(4)第二车间更换设备后,加工的商品的件数y与时间x的函数关系式为:y=100+100(x-2.8)=100x-180,
由(3)可知x=2.8时商品总和小于300件,
∴加工300件的时间超过2.8小时,
当<x≤4.8时,60x+100x-180=300,
解得:x=3,
∴经过3小时恰好装满第1箱,
当x=4.8时,60×4.8+300=588,
∴第二车间结束工作时加工的商品不够装满第2箱,
设再经过y小时恰好装满第二箱,由题意列方程得:
60y+100(4.8-3)=300,
解得:y=2,故符合题意,
答:经过3小时恰好装满第1箱,再经过2小时恰好装满第二箱.
点评 此题考查一次函数的应用,关键是根据题意列出方程和利用待定系数法得出解析式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
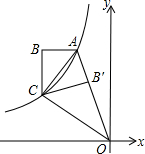 如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.
如图,双曲线y=-$\frac{3}{x}$(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,则三角形OAC的面积是$\frac{9}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | OA=OC,OB=OD | B. | AC=BD | ||
| C. | AC⊥BD | D. | ∠ABC=∠BCD=∠CDA=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
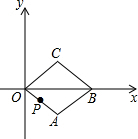 如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点B在x轴上,OA=1,∠AOC=60°.当菱形OABC开始以每秒转动60度的速度绕点O逆时针旋转时,动点P同时从点O出发,以每秒1个单位的速度沿菱形OABC的边逆时针运动.当运动时间为1秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当运动时间为2015秒时,点P的坐标是($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价格x(元/本) | … | 25 | 30 | 35 | 40 | … |
| 销售量y(本) | … | 250 | 200 | 150 | 100 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com