Question

4．O为△ABC内一点，BO、CO延长线分别交AC、AB于D、E，如果BE•BA+CD•CA=BC²．求证：A、D、O、E四点共圆．

Answer 1

分析 作∠CDF=∠ABC交CB于点F，连接EF，易得△CDF∽△CBA，得出CD•CA=CF•CB=CF•（CF+FB），由BE•BA+CD•CA=BC²，可得出BE•BA=BF•BC，从而得出△BEF∽△BCA，再利用角边关系可得出△CFE∽△DFB，相似三角形的对应角相等，可得∠ADB=∠BEC，从而得出∠ADB+∠AEC=∠BEC+∠AEC=180°，即可得出结论．

解答 解：如图，作∠CDF=∠ABC交CB于点F，连接EF，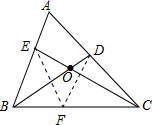

∵∠CDF=∠ABC，∠DCF=∠BCA，
∴△CDF∽△CBA，
∴$\frac{CD}{BC}$=$\frac{CF}{CA}$，即CD•CA=CF•CB=CF•（CF+FB），
∵BE•BA+CD•CA=BC²，
∴BE•BA=BC²-CD•CA=（CF+FB）²-CF•（CF+FB）=FB•（FB+CF）=BF•BC，
∵∠EBF=∠CAB，
∴△BEF∽△BCA，
∴△CDF∽△CBA∽△BEF，
∴$\frac{CF}{DF}$=$\frac{EF}{BF}$，即$\frac{CF}{EF}$=$\frac{DF}{BF}$，
又∵∠EFC=∠EFD+∠DFC=∠EFB+∠DFE=∠DFB．
∴△CFE∽△DFB，
∴∠ADB=∠DCF+∠DBF=∠BEF+∠CEF=∠BEC，
∴∠ADB+∠AEC=∠BEC+∠AEC=180°，
∴A，D，O，E四点共圆．

点评 本题主要考查了四点共圆，涉及相似三角形的判定与性质，四边形共圆的判定，解题的关键是正确作出辅助线，找出相似三角形．