
分析 需要分类讨论:①当点C位于x轴上时,根据线段间的和差关系即可求得点C的坐标;②当点C位于y轴上时,根据勾股定理求点C的坐标.
解答 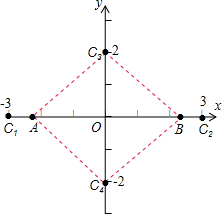 解:如图,①当点C位于y轴上时,设C(0,b).
解:如图,①当点C位于y轴上时,设C(0,b).
则$\sqrt{(\sqrt{5})^{2}+{b}^{2}}+\sqrt{(-\sqrt{5})^{2}+{b}^{2}}$=6,解得,b=2或b=-2,
此时C(0,2),或C(0,-2).
如图,②当点C位于x轴上时,设C(a,0).
则|-$\sqrt{5}$-a|+|a-$\sqrt{5}$|=6,即2a=6或-2a=6,
解得a=3或a=-3,
此时C(-3,0),或C(3,0).
综上所述,点C的坐标是:(0,2),(0,-2),(-3,0),(3,0).
故答案是4.
点评 本题考查了勾股定理、坐标与图形的性质.解题时,要分类讨论,以防漏解.另外,当点C在y轴上时,也可以根据两点间的距离公式来求点C的坐标.


科目:初中数学 来源: 题型:选择题
| A. | (4,-2) | B. | (2,4) | C. | (1,8) | D. | (-2,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
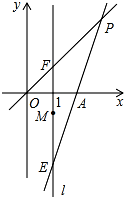 如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称.直线EA与直线OF交于点P.
如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称.直线EA与直线OF交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com