
分析 经判断该单位人数超过25人,设该单位共有x名员工去泰山旅游,由题意列出关于x的方程,求出方程的解即可得到结果.
解答 解:经判断该单位人数超过25人,设该单位共有x名员工去泰山旅游,
根据题意得:[800-10(x-25)]x=27000,
整理得:x2-105x+2700=0,即(x-60)(x-45)=0,
解得:x=60或x=45,
若x=60,每人团费为800-10×35=450(元)<550元,不合题意,舍去;
若x=45,每天团费为800-10×20=600(元)>550元,符合题意,
则该单位共有45名员工去泰山旅游.
点评 此题考查了一元二次方程的应用,正确理解“每超过1人,每人团费降低10元”是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1.5 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | 2 | C. | 4 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为15.
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为15.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
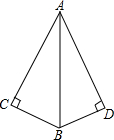 如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.
如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.| A. | AC=AD | B. | AB=AB | C. | ∠ABC=∠ABD | D. | ∠BAC=∠BAD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com