
【题目】如图所示,位于![]() 处的海上救援中心获悉:在其北偏东
处的海上救援中心获悉:在其北偏东![]() 方向的
方向的![]() 处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东
处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东![]() 相距
相距![]() 海里的
海里的![]() 处救生船,并通知救生船,遇险船在它的正东方向
处救生船,并通知救生船,遇险船在它的正东方向![]() 处,现救生船沿着航线
处,现救生船沿着航线![]() 前往
前往![]() 处救援,若救生船的速度为
处救援,若救生船的速度为![]() 海里/时,请问:
海里/时,请问:

![]() 到
到![]() 的最短距离是多少?
的最短距离是多少?
![]() 救生船到达
救生船到达![]() 处大约需要多长时间?(结果精确到
处大约需要多长时间?(结果精确到![]() 小时:参考数据:
小时:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() 到
到![]() 的最短距离是33.51海里,(2)救生船到达B处大约需要1.7小时.
的最短距离是33.51海里,(2)救生船到达B处大约需要1.7小时.
【解析】
(1)根据锐角三角函数可以求得CD和BD的长,从而可以解答本题;
(2)根据(1)中的结果可以解答本题.
(1)过点C作CD⊥AB,垂足为D.
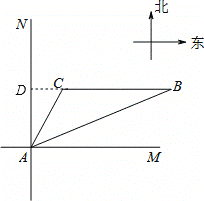
由题意知∠NAC=30°,∠NAB=68°,AC=20,
∴∠CAB=38°,∠BAM=90°—68°=22°,
∵BC∥AM,∴∠CBA=∠BAM=22°.
∵CD⊥AB,
∴∠ADC=∠CDB=90°.
在Rt△BCD中,sin∠CBD=![]() ,
,
∴CB=![]() ,
,
(2)救生船到达B处大约需要:t=![]() =1.7(小时).
=1.7(小时).
答:(1)![]() 到
到![]() 的最短距离是33.51海里,(2)救生船到达B处大约需要1.7小时.
的最短距离是33.51海里,(2)救生船到达B处大约需要1.7小时.


科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O、A2B2C2C1、A3B3C3C2…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3,…分别在直线 y=x+1 和 x 轴上,则点A2019 的坐标是( )
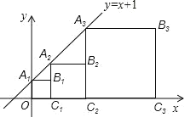
A.(22018 ,22019)B.(22018 1,22018)
C.(22019 ,22018)D.(22018 1,22019 )
查看答案和解析>>
科目:初中数学 来源: 题型:
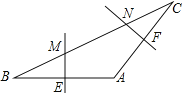
【题目】如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
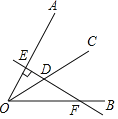
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示,若DE=1,则DF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC中,D为AC上一点,E为AB延长线上一点,DE⊥AC交BC于点F,且DF=EF.
(1)求证:CD=BE;
(2)若AB=12,试求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于二次三项式a2+2ab+b2,能直接用完全平方公式进行因式分解,得到结果为(a+b)2.而对于二次三项式a2+4ab﹣5b2,就不能直接用完全平方公式了,但我们可采用下述方法:
a2+4ab﹣5b2=a2+4ab+4b2﹣4b2﹣5b2=(a+2b)2﹣9b2,
=(a+2b﹣3b)(a+2b+3b)=(a﹣b)(a+5b).
像这样把二次三项式分解因式的方法叫做添(拆)项法.
解决问趣:
(1)请利用上述方法将二次三项式a2+6ab+8b2分解因式;
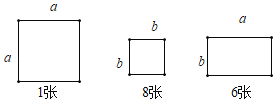
(2)如图,边长为a的正方形纸片1张,边长为b的正方形纸片8张,长为a,宽为b的长方形纸片6张,这些纸片可以拼成一个不重叠,无空隙的长方形图案,请画出示意图;
(3)已知x>0,且x≠2,试比较分式![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是二次函数![]() 的图象,其顶点坐标为
的图象,其顶点坐标为![]() .
.

![]() 求出图象与
求出图象与![]() 轴的交点
轴的交点![]() ,
,![]() 的坐标;
的坐标;
![]() 在二次函数的图象上是否存在点
在二次函数的图象上是否存在点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标;若不存在,请说明理由;
点的坐标;若不存在,请说明理由;
![]() 将二次函数的图象在
将二次函数的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线![]() 与此图象有两个公共点时,
与此图象有两个公共点时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com