
| A. | 等于0 | B. | 恒正 | C. | 恒负 | D. | 不能确定 |
分析 根据二次函数图象与x轴交点横坐标是相应方程的根可得b=-a(x1+x2)、c=ax1x2,代入函数解析式可得y=a[x2-(x1+x2)x+x1x2],根据点M(x0,y0)在x轴下方代入解析式可判断代数式值的情况.
解答 解:∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点坐标分别为(x1,0),(x2,0),
∴x1、x2是方程ax2+bx+c=0的两根,
∴x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,即b=-a(x1+x2),c=ax1x2,
则二次函数解析式可化为:y=ax2-a(x1+x2)x+ax1x2=a[x2-(x1+x2)x+x1x2],
∵图象上有一点M(x0,y0)在x轴下方,
∴当x=x0时,y<0,即a[x2-(x1+x2)x+x1x2]=a[x02-(x1+x2)x0+x1x2]<0,
当a<0时,x02-(x1+x2)x0+x1x2>0;
当a>0时,x02-(x1+x2)x0+x1x2<0,
故代数式代数式x02-(x1+x2)x0+x1x2的值不能确定,
故选:D.
点评 本题主要考查二次函数图象与x轴交点情况,熟知二次函数图象与x轴交点横坐标是相应一元二次方程的根是解题的基础和关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
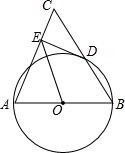 如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC于D.
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
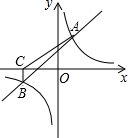 如图,一次函数y1=x+1与反比例函数y2=$\frac{k}{x}$的图象相交于点A(2,3)和点B.
如图,一次函数y1=x+1与反比例函数y2=$\frac{k}{x}$的图象相交于点A(2,3)和点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
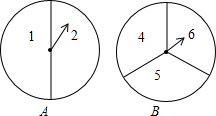 如图,有两个可以自由转动的均匀转盘A、B,分别被分成2等份和3等份,每份内均都有数字.小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘A和B,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.
如图,有两个可以自由转动的均匀转盘A、B,分别被分成2等份和3等份,每份内均都有数字.小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘A和B,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com