
【题目】阅读下面材料:
小敏遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使
问题得到解决(如图2).
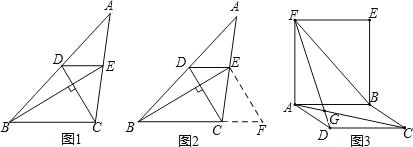
(1)请回答:BC+DE的值为 .
(2)参考小明思考问题的方法,解决问题:
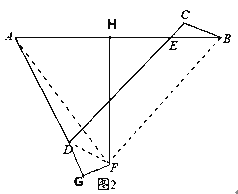
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
如图4,已知:AB、CD交于E点,连接AD、BC,AD=3![]() ,BC=1.且∠B与∠D互为余角,∠A与∠C互为补角,则∠AED= 度,若CD=
,BC=1.且∠B与∠D互为余角,∠A与∠C互为补角,则∠AED= 度,若CD=![]() ,求AB的长.
,求AB的长.

【答案】(1)![]() ;(2)∠AGF=60°,∠AED=45°,AB=7
;(2)∠AGF=60°,∠AED=45°,AB=7
【解析】试题分析:(1)由DE∥BC,EF∥DC,可证得四边形DCFE是平行四边形,求出DE=CF,DC=EF,由DC⊥BE,四边形DCFE是平行四边形,可得Rt△BEF,求出BF的长,证明BC+DE=BF;
(2)首先连接AE,CE,由四边形ABCD是平行四边形,四边形ABEF是矩形,易证得四边形DCEF是平行四边形,继而证得△ACE是等边三角形,则可求得答案.
以CD、CB为邻边作平行四边形BCDF,则有∠ABF=∠AED=45°,BF=DC=4![]() ,通过解直角三角形求解即可.
,通过解直角三角形求解即可.
试题解析:(1)∵DE∥BC,EF∥DC,
∴四边形DCFE是平行四边形,
∴EF=CD=3,CF=DE,
∵CD⊥BE,
∴EF⊥BE,
∴BC+DE=BC+CF=BF=![]()
(2)解决问题:连接AE,CE,如图.
∵四边形ABCD是平行四边形,
∴AB∥DC.
∵四边形ABEF是矩形,
∴AB∥FE,BF=AE.
∴DC∥FE.
∴四边形DCEF是平行四边形.
∴CE∥DF.
∵AC=BF=DF,
∴AC=AE=CE.
∴△ACE是等边三角形.
∴∠ACE=60°.
∵CE∥DF,
∴∠AGF=∠ACE=60°.
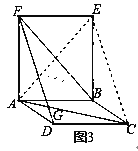
∵∠B与∠D互为余角,∠A与∠C互为补角,
∴∠D+∠B=90°,∠A+∠C=180°.
∵∠A+∠D+∠AED=180°,
∠B+∠C+∠BEC=180°,
∴∠A+∠D+∠AED+∠B+∠C+∠BEC=360°.
∴∠AED+∠BEC+90°+180°=360°.
∴∠AED+∠BEC=90°.
∵∠AED=∠BEC,
∴∠AED=∠BEC=45°.
以CD、CB为邻边作平行四边形BCDF,连接AF,如图2所示,
∵四边形BCDF是平行四边形,
∴BF=DC=4![]() ,DF=BC=1,∠DFB=∠C=180°﹣∠DAB,DC∥BF.
,DF=BC=1,∠DFB=∠C=180°﹣∠DAB,DC∥BF.
∴∠ABF=∠AED=45°.
在四边形ABFD中,
∵∠DAB+∠ABF+∠BFD+∠ADF=360°,∠DFB=180°﹣∠DAB,∠ABF=45°,
∴∠ADF=135°.
DF=1 , DG=FG=![]()
在△AGF中,
∵AG=3.5![]() ,DG=
,DG=![]() ,∠G=90°,
,∠G=90°,
∴AF=5
BF=4![]() ,FH=BH=4,AF=5,AH=3
,FH=BH=4,AF=5,AH=3
∴AB的长为7.


科目:初中数学 来源: 题型:
【题目】有5名同学进行体育测验,成绩分别是70,80,85,75,85(单位:分),这次体育测验成绩的众数和中位数分别是( )
A. 79分,85分B. 80分,79分C. 85分,80分D. 85分,85分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲队的平均成绩和方差;
(3)已知乙队成绩的方差是1 ![]() ,则成绩较为整齐的是哪一队.
,则成绩较为整齐的是哪一队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
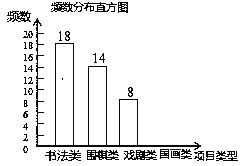
根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三军受命,我解放军各部队奋力抗战地救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到小镇只有唯一通道,且路程为24km,如图是他们行走的路线关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是( ) 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
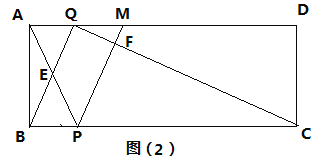
【题目】如图(1),矩形ABCD,AB=2cm,AD=6cm,P、Q分别为两个动点,点P从B出发沿边BC运动,每秒1cm,点Q从B出发沿边B—C—D运动,每秒2cm.
(1)若P、Q两点同时出发,其中一点到达终点时另一点也随之停止,设△BPQ面积为S,时间为t秒,求S关于t的函数关系式及自变量的取值范围;

(2)若R为AD中点,连接RP、RQ,当以R、P、Q为顶点的三角形与△BPQ相似(含全等)时,求t的值;
(3)如图(2)M为AD边上一点,AM=2,点Q在1.5秒时便停止运动,点P继续在BC上运动,AP与BQ交于点E,PM交CQ于点F,设四边形QEPF的面积为y,求y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com