[题目]化简:5(a2b3+ab2)﹣(2ab2+a2b3)．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】化简：5(a2b3+ab2)﹣(2ab2+a2b3)．

【答案】4a2b3+3ab2

【解析】

先去括号，再合并同类项即可；

解：原式=5a2b3+5ab2﹣2ab2﹣a2b3

=4a2b3+3ab2

练习册系列答案

湘教考苑高中学业水平考试模拟试卷系列答案

全程设计系列答案

小状元冲刺100分必选卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】阅读下面材料：

小敏遇到这样一个问题：如图1，在△ABC中，DE∥BC分别交AB于D，交AC于E．已知CD⊥BE，CD=3，BE=5，求BC+DE的值．

小明发现，过点E作EF∥DC，交BC延长线于点F，构造△BEF，经过推理和计算能够使

问题得到解决（如图2）．

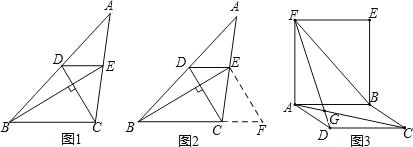
（1）请回答：BC+DE的值为　　．

（2）参考小明思考问题的方法，解决问题：

如图3，已知ABCD和矩形ABEF，AC与DF交于点G，AC=BF=DF，求∠AGF的度数．

如图4，已知：AB、CD交于E点，连接AD、BC，AD=3，BC=1．且∠B与∠D互为余角，∠A与∠C互为补角，则∠AED= 度，若CD=，求AB的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】若a+b＝2017，c+d＝﹣1，则（a﹣2c）﹣（2d﹣b）＝_______。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某工厂计划生产A、B两种产品共50件，需购买甲、乙两种材料．生产一件A产品需甲种材料30千克、乙种材料10千克；生产一件B产品需甲、乙两种材料各20千克．经测算，购买甲、乙两种材料各1千克共需资金40元，购买甲种材料2千克和乙种材料3千克共需资金105元．
（1）甲、乙两种材料每千克分别是多少元？
（2）现工厂用于购买甲、乙两种材料的资金不超过38000元，且生产B产品不少于28件，问符合条件的生产方案有哪几种？
（3）在（2）的条件下，若生产一件A产品需加工费200元，生产一件B产品需加工费300元，应选择哪种生产方案，使生产这50件产品的成本最低？（成本=材料费+加工费）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某步行街摆放有若干盆甲、乙、丙三种造型的盆景．甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成，乙种盆景由10朵红花和12朵黄花搭配而成，丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成．这些盆景一共用了2900朵红花，3750朵紫花，求黄花一共用了多少朵？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下列说法中，正确的个数有（　　） ①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为；
②直角三角形的最大边长为，最短边长为1，则另一边长为；
③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；
④等腰三角形面积为12，底边上的高为4，则腰长为5．
A.1个
B.2个
C.3个
D.4个