
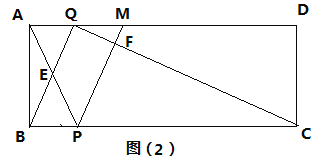
【题目】如图(1),矩形ABCD,AB=2cm,AD=6cm,P、Q分别为两个动点,点P从B出发沿边BC运动,每秒1cm,点Q从B出发沿边B—C—D运动,每秒2cm.
(1)若P、Q两点同时出发,其中一点到达终点时另一点也随之停止,设△BPQ面积为S,时间为t秒,求S关于t的函数关系式及自变量的取值范围;

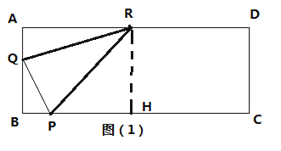
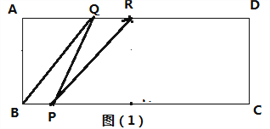
(2)若R为AD中点,连接RP、RQ,当以R、P、Q为顶点的三角形与△BPQ相似(含全等)时,求t的值;
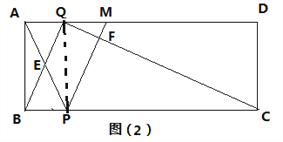
(3)如图(2)M为AD边上一点,AM=2,点Q在1.5秒时便停止运动,点P继续在BC上运动,AP与BQ交于点E,PM交CQ于点F,设四边形QEPF的面积为y,求y的最大值.
【答案】(1)![]() ,
, ![]() ;(2)t=0.25或
;(2)t=0.25或![]() ;(3)
;(3)![]()
【解析】(1)根据矩形的对边相等表示出BC,然后表示出PB、QB,再根据三角形的面积列式整理即可得解,根据点Q先到达终点确定出x的取值范围即可;
(2)进行分类讨论求解即可;
(3)根据面积计算得出函数关系式,再求出最大值 即可.
试题解析:(1) ![]()
![]()
(2)当∠RQP=90时,△ARQ∽△BQP, ![]() ,AQ=1.5,BQ=0.5,t=0.25
,AQ=1.5,BQ=0.5,t=0.25
当∠QPR=90时,△HPR∽△BQP, ![]() ,PH=4 不成立
,PH=4 不成立
当Q在AR上时,若QR=BP,则△RPQ全等于△BQP, ![]() ,
, ![]()
(3)连接PQ,则BP=t,则PC=6﹣x,
∵AM∥DP,
∴![]() ,
,
∴![]()
∵S△APQ=![]() ABAQ=t,
ABAQ=t,
∴S△abe=![]() ,
,
同理可得,S△PQF=![]() ,
,
∴y=![]() +
+![]() =
=![]()
![]()
当t=3时,上式等号成立,
∴y的最大值为: ![]() .
.


科目:初中数学 来源: 题型:
【题目】下列给出的四个命题:
①若 ![]() ,则
,则 ![]() ;②若
;②若 ![]() ,则
,则 ![]() ;
;
③ ![]() ;
;
④若方程 ![]() 的两个实数根中有且只有一个根为0,那么
的两个实数根中有且只有一个根为0,那么 ![]() .
.
其中是真命题是( )
A.①②
B.②③
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年百色市九年级参加中考人数约有38900人,数据38900用科学记数法表示为( )
A.3.89×102
B.389×102
C.3.89×104
D.3.89×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小敏遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使
问题得到解决(如图2).
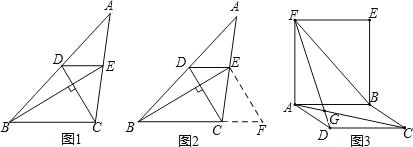
(1)请回答:BC+DE的值为 .
(2)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
如图4,已知:AB、CD交于E点,连接AD、BC,AD=3![]() ,BC=1.且∠B与∠D互为余角,∠A与∠C互为补角,则∠AED= 度,若CD=
,BC=1.且∠B与∠D互为余角,∠A与∠C互为补角,则∠AED= 度,若CD=![]() ,求AB的长.
,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,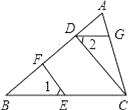
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运动中,属于平移的是( )
A. 冷水加热过程中,小气泡上升成为大气泡 B. 急刹车时汽车在地面上的滑动
C. 随手抛出的彩球运动 D. 随风飘动的风筝在空中的运动
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2+2kx+k2﹣6=0
(1)证明:方程有两个不相等的实数根;
(2)如果方程有一个根为2,试求2k2+8k+2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当△BCP的面积最大时,求点P的坐标和△BCP的最大面积.
(3)当△BCP的面积最大时,在抛物线上是否点Q(异于点P),使△BCQ的面积等于△BCP,若存在,求出点Q的坐标,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com