练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，隧道的截面由抛物线和长方形构成，长方形的长是8m，宽是2m，抛物线的最高点到路面的距离为6米．

    （1）按如图所示建立平面直角坐标系，求表示该抛物线的函数表达式；

    （2）一辆货运卡车高为4m，宽为2m，如果该隧道内设双向车道，那么这辆货车能否安全通过？

    【答案】（1）y=﹣（x﹣4）2+6；（2）这辆货车能安全通过．

    【解析】试题分析：（1）根据题意可知顶点坐标和点B坐标，设抛物线的函数表达式为顶点式，代入即可求出表达式；

    （2）利用宽2m求出高为5m，所以可以通过．

    试题解析：解：（1）如图1，由题意得：最高点C（4，6），B（8，2），设抛物线的函数表达式：y=a（x﹣4）2+6，把（8，2）代入得：a（8﹣4）2+6=2，a=﹣，∴y=﹣（x﹣4）2+6；

    （2）如图2，当DE=2时，AD=AE﹣DE=4﹣2=2，当x=2时，y=﹣（2﹣4）2+6=5＞4，∴这辆货车能安全通过．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，在中，与的平分线交于点，过点作交于点，交于点，那么下列结论：①；②；③和都是等腰三角形；④的周长等于与的和，其中正确的有(　　)

    A.4个B.3个C.2个D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，四边形ABCD是正方形，M是AB延长线上一点．直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A、B重合），另一直角边与∠CBM的平分线BF相交于点F．

    （1）如图1，当点E在AB边得中点位置时：

    ①通过测量DE、EF的长度，猜想DE与EF满足的数量关系是 ．

    ②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是 ，请证明你的猜想．

    （2）如图2，当点E在AB边上的任意位置时，猜想此时DE与EF有怎样的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB＝12，点E是AD上的一点，AE＝6，BE的垂直平分线交BC的延长线于点F，连接EF交CD于点G．若G是CD的中点，则BC的长是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明袋子中有1个红球和3个白球，这些球除颜色外都相同．

    （1）从袋中任意摸出2个球，用树状图或列表求摸出的2个球颜色不同的概率；

    （2）在袋子中再放入x个白球后，进行如下实验：从袋中随机摸出1个球，记录下颜色后放回袋子中并搅匀．经大量试验，发现摸到白球的频率稳定在0.95左右，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．

    求证：（1）△AFD≌△CEB．（2）四边形ABCD是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

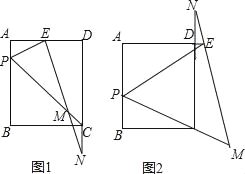
    【题目】如图1，矩形ABCD中，P是AB边上的一点（不与A，B重合），PE平分∠APC交射线AD于E，过E作EM⊥PE交直线CP于M，交直线CD于N．

    （1）求证：CM=CN；

    （2）若AB：BC=4：3，

    ①当=　 　时，E恰好是AD的中点；

    ②如图2，当△PEM与△PBC相似时，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB与CD交于点O，OE平分∠AOC，点F为AB上一点(不与点A及O重合)，过点F作FG∥OE，交CD于点G，若∠AOD＝110°，则∠AFG度数为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知将一副三角板（直角三角板OAB和直角三角板OCD，∠AOB=90°，∠ABO=45°，∠CDO=90°，∠COD=60°）

    （1）如图1摆放，点O、A、C在一直线上，则∠BOD的度数是多少？

    （2）如图2，将直角三角板OCD绕点O逆时针方向转动，若要OB恰好平分∠COD，则∠AOC的度数是多少？

    （3）如图3，当三角板OCD摆放在∠AOB内部时，作射线OM平分∠AOC，射线ON平分∠BOD，如果三角板OCD在∠AOB内绕点O任意转动，∠MON的度数是否发生变化？如果不变，求其值；如果变化，说明理由．

    查看答案和解析>>

    同步练习册答案