
【题目】如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G.若G是CD的中点,则BC的长是__________.

【答案】10.5
【解析】
利用ASA定理证明△EDG≌△FCG,从而求得DE=CF,EG=GF=![]() ,根据矩形的性质,设BC=x,则DE=x-6,DG=6,BF=2x-6,根据垂直平分线的性质求得EG=
,根据矩形的性质,设BC=x,则DE=x-6,DG=6,BF=2x-6,根据垂直平分线的性质求得EG=![]() ,然后根据勾股定理列方程求解即可.
,然后根据勾股定理列方程求解即可.
解:在矩形ABCD中,AD=BC,AB=CD=12,∠D=∠DCF=90°
∵G为CD中点,∴DG=CG
又∵∠EGD=∠FGC
∴△EDG≌△FCG
∴DE=CF,EG=GF=![]()
设BC=x,则DE=AD-AE=BC-AE=x-6,DG=CG=![]() =6,BF=BC+CF=BC+DE=2x-6,
=6,BF=BC+CF=BC+DE=2x-6,
又∵BE的垂直平分线交BC的延长线于点F,
∴EG=GF=![]()
∴在Rt△EDG中,![]()
解得:x=10.5
则BC的长是10.5
故答案为:10.5.



 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,分别以AC,BC为边在AB的同侧作等边△HAC与等边△DCB,连接DH.
(1)如图1,当∠DHC=90°时,求![]() 的值;
的值;
(2)在(1)的条件下,作点C关于直线DH的对称点E,连接AE,BE.求证:CE平分∠AEB.
(3)现将图1中的△DCB绕点C顺时针旋转一定角度α(0°<α<90°),如图2,点C关于直线DH的对称点为E,则(2)中的结论是否还成立,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
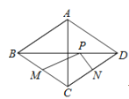
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.
(1)按如图所示建立平面直角坐标系,求表示该抛物线的函数表达式;
(2)一辆货运卡车高为4m,宽为2m,如果该隧道内设双向车道,那么这辆货车能否安全通过?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,
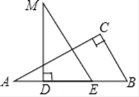
(1)试说明△ABC与△MED全等;
(2)若∠M=35°,求∠B的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三八妇女节到来之际,某学校准备让办公室的王老师去给女教师们买点糖果作为礼物.王老师预先了解到目前比较受老师们喜爱的![]() ,
,![]() 两种糖果的价格之和为140元,他计划购买
两种糖果的价格之和为140元,他计划购买![]() 糖果的数量比
糖果的数量比![]() 糖果的数量多5盒,但一共不超过60盒,正当王老师去超市买糖果的时候,发现
糖果的数量多5盒,但一共不超过60盒,正当王老师去超市买糖果的时候,发现![]() 正打九折销售,而
正打九折销售,而![]() 的价格提高了10%,王老师决定将
的价格提高了10%,王老师决定将![]() ,
,![]() 糖果的购买数量对调,这样,实际花费只比原计划多20元.已知价格和购买数量均为整数,则王老师原计划购买糖果的总花费为________元.
糖果的购买数量对调,这样,实际花费只比原计划多20元.已知价格和购买数量均为整数,则王老师原计划购买糖果的总花费为________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com