
(本题满分12分)在平面直角坐标系 中,点M(
中,点M( ,
, ),以点M为圆心,OM长为半径作⊙M .使⊙M与直线OM的另一交点为点B,与
),以点M为圆心,OM长为半径作⊙M .使⊙M与直线OM的另一交点为点B,与 轴、
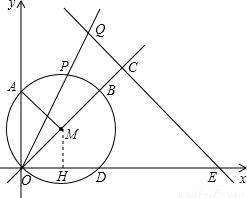
轴、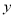 轴的另一交点分别为点D、A(如图),连接AM.点P是
轴的另一交点分别为点D、A(如图),连接AM.点P是 上的动点.
上的动点.

(1)∠AOB的度数为 .
(2)Q是射线OP上的点,过点Q作QC垂直于直线OM,垂足为C,直线QC交 轴于点E.
轴于点E.
①当QE与⊙M相切时,求点E的坐标;
②在①的条件下,在点P运动的整个过程中,求△ODQ面积的最大值及点Q经过的路径长.
(1)45°;(2)①E点坐标为( ,0);②△ODQ面积的最大值为8,Q经过的路径长为4.
,0);②△ODQ面积的最大值为8,Q经过的路径长为4.
【解析】
试题分析:(1)首先过点M作MH⊥OD于点H,由点M(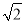 ,
,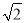 ),可得∠MOH=45°,OH=MH=
),可得∠MOH=45°,OH=MH=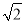 ,继而求得∠AOM=45°;
,继而求得∠AOM=45°;
(2)①由OH=MH=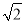 ,MH⊥OD,即可求得OD与OM的值,继而可得OB的长,由于QE与⊙M相切,所以B与C重合,故△OBE为等腰直角三角形,从而得到OE=
,MH⊥OD,即可求得OD与OM的值,继而可得OB的长,由于QE与⊙M相切,所以B与C重合,故△OBE为等腰直角三角形,从而得到OE=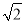 OB=
OB= ,得到点E的坐标;
,得到点E的坐标;
②由OD=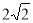 ,Q的纵坐标为t,即可得S=
,Q的纵坐标为t,即可得S=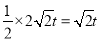 ,当动点P与A点重合时,Q点与y轴上R点重合,此时Q点的纵坐标最大,可求得OQ的长,继而求得△ODQ的最大面积;由已知可得:Q在线段BR上运动,显然BR=OB=4.
,当动点P与A点重合时,Q点与y轴上R点重合,此时Q点的纵坐标最大,可求得OQ的长,继而求得△ODQ的最大面积;由已知可得:Q在线段BR上运动,显然BR=OB=4.
试题解析:(1)过点M作MH⊥OD于点H,
∵点M( ,
, ),∴OH=MH=
),∴OH=MH= ,∴∠MOD=45°,∵∠AOD=90°,∴∠AOM=45°;
,∴∠MOD=45°,∵∠AOD=90°,∴∠AOM=45°;
(2)①∵OH=MH= ,MH⊥OD,
,MH⊥OD,
∴OM=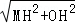 =2,OD=2OH=
=2,OD=2OH=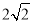 ,
,
∴OB=4,
∵QE与⊙M相切,∴B与C重合,∴△OBE为等腰直角三角形,∴OE= OB=
OB= ,
,
∴E点坐标为( ,0)
,0)
②∵OD=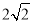 ,Q的纵坐标为t,∴S=
,Q的纵坐标为t,∴S=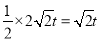 .
.
如图2,当动点P与A点重合时,Q点与y轴上R点重合,此时Q点的纵坐标最大,
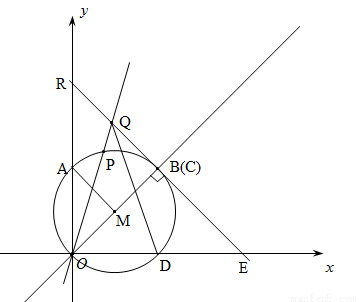
∵∠AOM=45°,OB=4,∠OBR=90°,∴BR=OB=4,∴OR= ,∴
,∴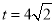 ,
,
∴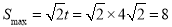 .
.
∵Q只能在线段BR上运动.∴Q经过的路径长为BR=4.
考点:圆的综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年江苏省泰州市海陵区九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,PA、PB分别切⊙O于点A、B,若∠P=70°,点C为⊙O上任一动点,则∠C的大小为 °.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市海陵区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题10分).如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,其中点B坐标为(4,3).
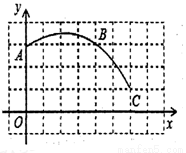
(1)请写出该圆弧所在圆的圆心D的坐标 .
(2)⊙D的半径为 ;
(3)求弧 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片八年级上学期期中考试数学试卷(解析版) 题型:选择题
下列结论错误的是( )
A.全等三角形对应边上的中线相等
B.两个直角三角形中,两个锐角相等,则这两个三角形全等
C.全等三角形对应边上的高相等
D.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com