
【题目】抛物线y=﹣![]() x2+ax+b交x轴于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是抛物线在第一象限上的一点,过点P作AC的平行线l,分别交直线BC,y轴于点D,点E.
x2+ax+b交x轴于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是抛物线在第一象限上的一点,过点P作AC的平行线l,分别交直线BC,y轴于点D,点E.
(1)填空:直线AC的解析式为 ,抛物线的解析式为 ;
(2)当CD=![]() 时,求OE的长;
时,求OE的长;
(3)当DP=DE时,求点P的横坐标.
【答案】(1)y=2x+4,抛物线的解析式为![]() ;(2)OE的长为1;(3)点P的横坐标1
;(2)OE的长为1;(3)点P的横坐标1
【解析】
(1)先用待定系数法求出抛物线解析式,然后求出点、C坐标,再求直线AC的解析式即可;
(2)作BF//y轴,交DE于F.求出直线DE的解析式,表示出CE、BF的长,利用△CDE∽△BDF,列式求解即可;
(3)作PG//y轴,交BC于G.由△CED≌△GPD,可得PG=CE.求出直线BC的解析式,根据PG=CE列方程求解即可.
(1)把A(﹣2,0),B(4,0)代入y=﹣![]() x2+ax+b得,
x2+ax+b得,
![]() ,
,
解得
![]() ,
,
∴![]() .
.
当x=0时,y=4,
∴C(0,4),
设直线AC的解析式为y=mx+n,
![]() ,
,
![]() ,
,
∴y=2x+4;
(2)如图,作BF//y轴,交DE于F.
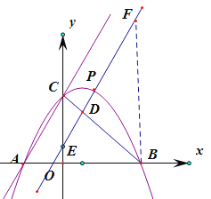
∵B(4,0),C(0,4),
∴BC=4![]() ,
,
∵CD=![]() ,
,
∴BD=3![]() .
.
设DE的解析式为y=2x+b,则E(0,b),CE=4-b,
当x=4时,y=8+b,则BF=8+b,
∵BF//y轴,
∴△CDE∽△BDF,
∴![]() ,
,
∴![]() ,
,
解得
b=1,
∴OE=1;
(3)如图,作PG//y轴,交BC于G.
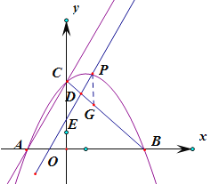
∵PG//y轴,
∴∠CED=∠GPD, ∠ECD=∠PGD,
∵DP=DE,
∴△CED≌△GPD,
∴PG=CE.
设直线BC的解析式为y=ax+c,
∵B(4,0),C(0,4),
∴![]() ,
,
解得
![]() ,
,
∴y=-x+4.
设P(m, ![]() ),G(m,
),G(m, ![]() ),
),
把P(m, ![]() )代入y=2x+b得
)代入y=2x+b得
2m+b=![]() ,
,
∴b=![]() ,
,
∴4-(![]() )=
)=![]() -(
-(![]() ),
),
m2-m=0,
解得
m1=0(舍去),m2=1,
∴点P的横坐标1.


科目:初中数学 来源: 题型:
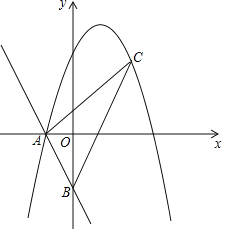
【题目】一次函数y=﹣2x﹣2分别与x轴、y轴交于点A、B.顶点为(1,4)的抛物线经过点A.
(1)求抛物线的解析式;
(2)点C为第一象限抛物线上一动点.设点C的横坐标为m,△ABC的面积为S.当m为何值时,S的值最大,并求S的最大值;
(3)在(2)的结论下,若点M在y轴上,△ACM为直角三角形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点(1,0),且对称轴为直线
经过点(1,0),且对称轴为直线![]() ,其部分图象如图所示.对于此抛物线有如下四个结论:①
,其部分图象如图所示.对于此抛物线有如下四个结论:①![]() <0; ②
<0; ②![]() ;③9a-3b+c=0;④若
;③9a-3b+c=0;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确结论的序号是( )
时的函数值.其中正确结论的序号是( )
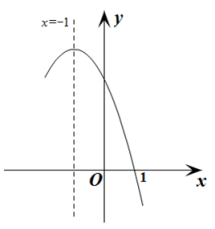
A.①③B.②④C.②③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
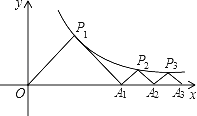
【题目】如图,P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)均在函数y=![]() (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,且斜边OA1、A1A2、A2A3…An﹣1An都在x轴上,则点P2的坐标是_____.
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,且斜边OA1、A1A2、A2A3…An﹣1An都在x轴上,则点P2的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
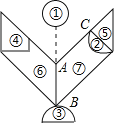
【题目】七巧板是我国古老的益智玩具,受到全世界人的追捧.下图是由一副“现代智力七巧板经无缝拼接且没有重叠的轴对称花朵型图案,直线AB为对称轴,其中①②③是直径为1的圆与半圆,④为直角梯形,⑤为等腰直角三角形,⑥⑦是有一组对边平行且锐角皆为45°的拼板.若已知④的周长是AB的3倍,⑥的周长是AB的5倍,则图中线段AC的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形 ![]() 中,点
中,点![]() 是射线
是射线 ![]() 上一个动点.连接
上一个动点.连接![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() .
.
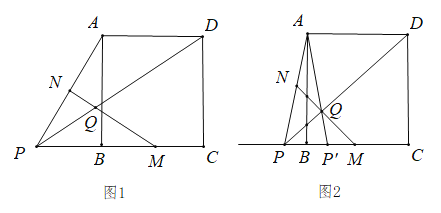
(1)如图 1,当点![]() 在线段
在线段 ![]() 的延长线上时,请判断
的延长线上时,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)如图 2,正方形 的边长为 4,点![]() 与点
与点![]() 关于直线
关于直线 ![]() 对称,且点
对称,且点![]() 在线段
在线段 ![]() 上.连接
上.连接![]() ,若点
,若点 ![]() 恰好在直线
恰好在直线![]() 上,求
上,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+(3b+1)x+b﹣3(a>0),若存在实数m,使得点P(m,m)在该抛物线上,我们称点P(m,m)是这个抛物线上的一个“和谐点”.
(1)当a=2,b=1时,求该抛物线的“和谐点”;
(2)若对于任意实数b,抛物线上恒有两个不同的“和谐点”A、B.
①求实数a的取值范围;
②若点A,B关于直线y=﹣x﹣(![]() +1)对称,求实数b的最小值.
+1)对称,求实数b的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com